Что такое активное сопротивление катушки

Закон электромагнитной индукции Фарадея

Формула магнитного потока

Отрицательное значение ЭДС – это обозначение противоположного знака по отношению к изменению Ф. Если скажут «запишите формулу закона электромагнитной индукции», следует не забывать о динамической природе рассматриваемого явления. Ниже приведены примеры для вычисления основных электрических параметров:

• ЭДС одиночного контура E1 = – (ΔФ/Δt), где Δt – временной интервал;
• при создании конструкции из N витков EN = – N*(ΔФ/Δt);
• ток в проводнике (замкнутый контур с электрическим сопротивлением R) I = E/R;
• движущийся со скоростью v проводник длиной D создает ЭДС E = В * D * v * sin α.

Разновидности катушек индуктивности

Контурные катушки индуктивности

Эти катушки используются совместно с конденсаторами для получения резонансных контуров. Они должны иметь высокую стабильность, точность идобротность .

Катушки связи

Такие катушки применяются для обеспечения индуктивной связи между отдельными цепями и каскадами. Такая связь позволяет разделить по постоянному току цепи базы иколлектора и т. д. К таким катушкам не предъявляются жёсткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и коэффициент связи.

Вариометры

Это катушки, индуктивность которых можно изменять в процессе эксплуатации для перестройки колебательных контуров. Они состоят из двух катушек, соединённых последовательно. Одна из катушек неподвижная (статор), другая располагается внутри первой и вращается (ротор). При изменении положения ротора относительно статора изменяется величина взаимоиндукции, а следовательно, индуктивность вариометра. Такая система позволяет изменять индуктивность в 4 − 5 раз. В ферровариометрах индуктивность изменяется перемещением ферромагнитного сердечника.

Дроссели

Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному. Обычно включаются в цепях питания усилительных устройств. Предназначены для защиты источников питания от попадания в них высокочастотных сигналов. На низких частотах они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники.

Сдвоенный дроссель

Сдвоенные дроссели

две намотанных встречно катушки индуктивности, используются в фильтрах питания. За счёт встречной намотки и взаимной индукции более эффективны при тех же габаритных размерах. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания; в дифференциальных сигнальных фильтрах цифровых линий, а также в звуковой технике.

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.

Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где

• Xl — индуктивность;
• Xс — ёмкость;
• R — активная составляющая.

Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

• X > 0, в элементе проявляются индуктивные свойства;
• X = 0, в ёмкости присутствует только активная величина;
• X < 0, в элементе проявляется ёмкостное сопротивление.

Будет интересно Что такое полярность конденсатора и как ее определить?

Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.

Импеданс элемента.

Формула расчета реактивного сопротивления

В общем случае для деталей катушечного типа применяются выражения:

X = L*w = 2* π*f*L.

Для конденсаторов применяют формулы:

X = 1/(w*C)= 1/(2* π*f*C).

Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.

Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.

Для чего она нужна и где используется

Подобные элементы находят множество применений, но наиболее часто они используются в качестве:

• Элементов индуктивности в слаботочных электрических цепях;
• Реакторов в силовой электронике, в качестве элементов компенсации реактивного характера нагрузки;
• Дросселей для сглаживания пульсаций выпрямленного или переменного тока;
• Электромагнитов в качестве источников магнитного поля в электромагнитных реле или органах управления различных устройств;
• Индукторов в установках индукционного нагрева;
• Накопителя энергии в источниках преобразования напряжения;
• Датчиков магнитных полей (магнитные головки в накопителях на жестких магнитных дисках);
• Линий задержки сигнала;
• Антенн для приема и передачи электромагнитных волн.

Индуктивная антенна

Самоиндукция

Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.

Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток L — индуктивность контура I — сила тока в контуре

Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.

Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.

Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.

Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:

• первая лампа загорится практически сразу,
• вторая лампа загорится с заметным запаздыванием.

При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.

ЭДС самоиндукции ξis — ЭДС самоиндукции ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность

Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.

Задачи на переменный электрический ток

Прежде, чем мы перейдем непосредственно к примерам решения задач на переменный ток, скажем кое-что для тех, кто вообще не знает, с какой стороны подступиться к задачам по физике. У нас есть универсальный ответ – памятка по решению. А еще, вам могут пригодиться формулы.

Хотите разобраться в теории? Читайте в нашем блоге, что такое фаза и ноль в электричестве.

Задача№1. Переменный ток

Условие

Вольтметр, включённый в цепь переменного тока,показывает напряжение 220 В, а амперметр – ток 10 А.Чему равны амплитудные значения измеряемых величин?

Решение

Амперметр показывает мгновенные, действующие значения величин. Действующие значения силы тока и напряжения меньше амплитудных в 2 раз. Исходя из этого, рассчитаем:

IA=Iд·2=10·2=14,1 АUA=Uд·2=220·2=311 В

Ответ: 14,1 А; 311 В.

Задача№2. Переменный ток

Условие

Рамка вращается в однородном магнитном поле. ЭДС индукции, возникающая в рамке, изменяется по закону e=80sin25πt. Определите время одного оборота рамки.

Решение

Из условия можно найти угловую частоту вращения рамки:

e=εmsinωte=80sin25πtω=25π радс

Время одного оборота рамки – это период колебаний, связанный с угловой частотой:

T=2πω=2π25π=,08 с

Ответ: 0,08 с.

Больше задач на тему ЭДС в нашем блоге.

Задача№3. Переменный ток

Условие

Сила тока в колебательном контуре изменяется по закону I =0,4sin(400πt) (А). Определите емкосьть конденсатора в контуре, если индуктивность катушки равна 125 мГн.

Решение

Запишем закон изменения силы тока в контуре:

I=IAsinωt

Учитывая исходное уравнение, можно найти угловую частоту и период колебаний:

ω=400π радс

T=2πω=2π400π=5·10-3c

Емкость конденсатора найдем из формулы Томпсона:

T=2πLCT2=4π2LCC=T24π2L=25·10-64·9,85·125·10-3=5·10-6 Ф

Ответ: 5 мкФ.

Задача№4. Переменный ток

Условие

Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?

Решение

Запишем закон Ома для цепи переменного тока:

I=UZ

Z – полное сопротивление цепи, которое складывается из активного и реактивного сопротивлений.

Z=R2+Xc2Xc=12πϑC

Найдем полное сопротивление, подставив в формулу данные из условия:

X=12·3.14·50·1·10-6=3,18 кОмZ=12·106+3,22·106=3,3 кОм

Далее по действующему значению напряжения найдем амплитудное:

UA=Uд·2=220·2=311 В

Теперь подставим апмлитудное значение напряжения в выражение для закона Ома и вычислим силу тока:

IA=UAZ=3113,3·103=,09 А

Ответ: 0,09 А.

Задача№5. Переменный ток

Условие

Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока с частотой 50 Гц. При напряжении 125 В сила тока равна 3 А. Какова индуктивность катушки?

Решение

В данной задаче, исходя из условия, можно пренебречь активным сопротивлением катушки. Ее индуктивное сопротивоение равно:

xL=ωL

По закону Ома:

U=IxL=IωL

Отсюда находим индуктивность:

L=UIω=1253·314=,13 Гн

Ответ: 0,13 Гн.

Все еще мало задач? Держите несколько примеров на мощность тока.

Определение взаимоиндуктивного сопротивления

Рассматривая две индуктивно-связанные катушки, запишем выражения э. д. с. самоиндукции и взаимоиндукции, возникающие при синусоидальных токах в обеих катушках, направленных одинаково относительно одноименных зажимов. Э. д. с. и напряжения:
от самоиндукции                                              от взаимоиндукции
в первой катушке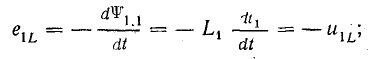    

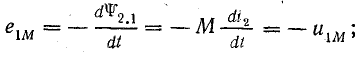
во второй катушке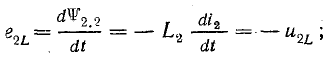    

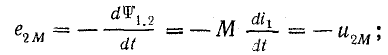
Э. д. с. и напряжения самоиндукции и взаимоиндукции имеют одинаковые знаки так как при согласном включении потоки самоиндукции и взаимоиндукции направлены одинаково. Создаваемый ими эффект противодействия току учитывается введением в расчет индуктивного сопротивления ωL₁, ωL₂ и взаимоиндуктивного сопротивления ωМ.
При встречном включении катушек э. д. с. и напряжения самоиндукции и взаимоиндукции будут иметь разные знаки:

Комплексные индуктивное и взаимоиндуктивное сопротивления записывают аналогично:

Задача 16.1.

Для определения параметров двух магнитно-связанных катушек провели измерения.
1. По схеме рис. 16.3, а измерили ток и напряжение на каждой катушке, включив их последовательно в сеть постоянного тока:

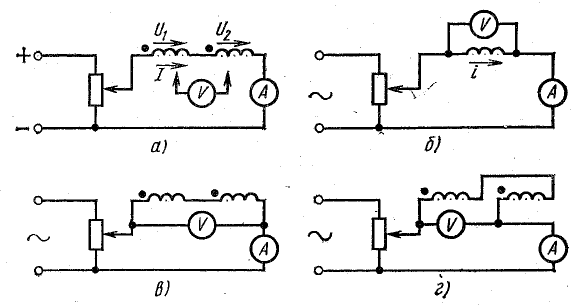
Рис. 16.3. К задаче 16.1

2.    По схеме рис. 16.3, б измерили в каждой катушке ток и напряжение, включив их порознь в сеть переменного тока: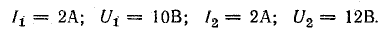
3.    По схеме рис. 16.3, в измерили ток и напряжение, включив катушки согласно и последовательно в сеть переменного тока:
4.    По схеме рис. 16.3, г измерили ток и напряжение, включив катушки встречно и последовательно в сеть переменного тока:

Определить активные сопротивления, индуктивности и взаимоиндуктивность катушек, если частота в сети переменного тока 50 Гц.Решение. Первый опыт позволяет определить активные сопротивления катушек, пренебрегая увеличением сопротивления от поверхностного эффекта: 
Второй опыт позволяет определить полные сопротивления катушек переменному току при отсутствии взаимного влияния, а затем рассчитать индуктивности: 
Индуктивные сопротивления: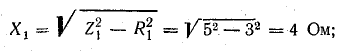
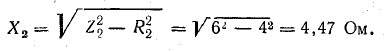
Индуктивности: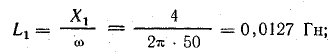
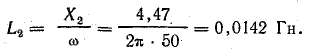
По результатам третьего и четвертого опытов определим взаимную индуктивность.
При согласном включении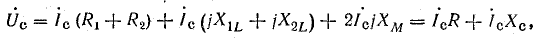
где

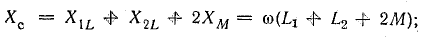
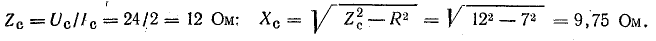   9,75 Ом.

При встречном включении

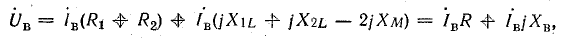
где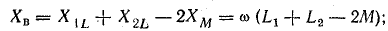  

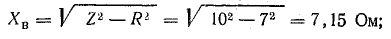
Вычтем второе уравнение из первого: .

Магнитный поток

Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.

Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.

Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению:

• модуля вектора магнитной индукции ​B​,
• площади поверхности ​S​, которую пронизывает поток,
• и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).

Магнитный поток Ф — магнитный поток B — магнитная индукция S — площадь пронизываемой поверхности n — вектор нормали (перпендикуляр к поверхности)

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента  — резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим.  Как нам говорит вики-словарь, «активный  — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

Последовательное соединение RC

Конденсаторы очень часто включают последовательно с сопротивлениями, но если даже специального сопротивления нет, любой конденсатор обладает определённой величиной активного сопротивления, которую необходимо учитывать в точных расчетах. Есть понятие “добротность” конденсатора, которая проявляет  активную составляющую его сопротивления

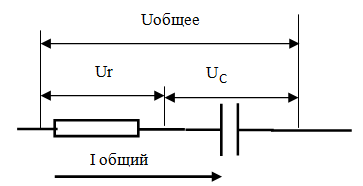
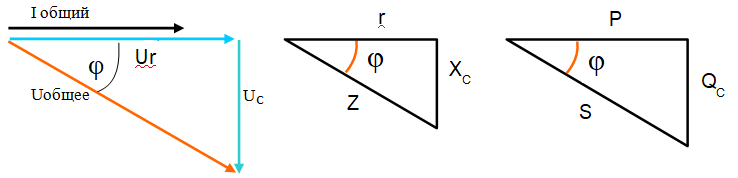
При последовательном соединении, через все элементы цепи протекает один ток, который называем – общий.

Сначала откладываем вектор тока, фазу которого принимаем равной нулю. Вектор напряжения на активном сопротивлении, откладываем в том же направлении, так как на активном сопротивлении ток и напряжение совпадают по фазе.

К концу вектора напряжения на активном сопротивлении прикладываем начало вектора напряжения на емкости. Фаза напряжения на емкости отстает от фазы напряжения на активном сопротивлении на 90 градусов, а вектор отстающего напряжения откладывается вниз.

Векторная диаграмма напряжений представляет собой прямоугольный треугольник, который позволяет определить все составляющие по теореме Пифагора.

Активное сопротивление R включенное в цепь с катушкой или конденсатором уменьшает угол сдвига фаз.

Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление обозначается буквой Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и X_С

Z 2 = Rа2 + X2_С

В цепи L C, в отличие от цепи только с C, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.

Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и Q_С

S2 = Р2 + Q2_С

Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников

Активное сопротивление катушки

Активное сопротивление обуславливается омической характеристикой проводов обмотки. При работе на низких частотах, омическое сопротивление не зависит от частоты. В мощных устройствах необходимо учитывать эффект близости, который заключается в том, что токи и образуемое ими магнитное поле вызывают вытеснение тока в проводах соседних витков. В результате, снижается эффективное используемое сечение провода и растет его омическое сопротивление.

Обратите внимание! На высоких частотах проявляется скин-эффект, который заключается в том, что ток вытесняется в поверхностные слои провода. В результате этого снижается используемое сечение кабеля

Для снижения скин-эффекта вместо одного проводника используют жгут из нескольких более тонких – литцендрат, либо поверхность провода покрывают слоем серебра, поскольку оно обладает наименьшим удельным сопротивлением.

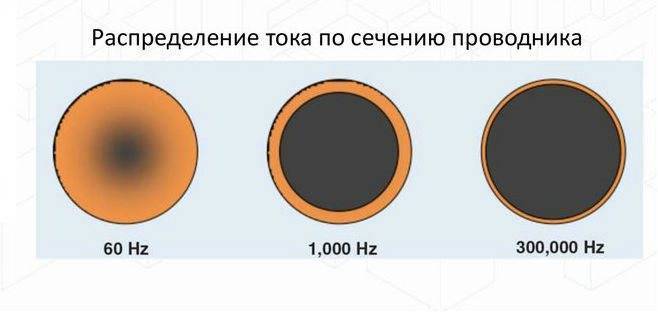
Скин-эффект

В мощных электромагнитных системах (ускорители частиц) для снижения активного сопротивления, используется свойство сверхпроводимости – полное исчезновение сопротивления при охлаждении некоторых материалов ниже критической температуры.

Провод литцендрат

Во многих случаях применения катушек индуктивности следует учитывать влияние активного сопротивления обмоток. Данный параметр может отрицательно влиять не только путем снижения добротности, но и вызывать повышенный нагрев проводников обмоток в том случае, когда устройство работает с большими токами.

Взаимоиндуктивное сопротивление

Сопротивление в электрической цепи, обусловленное взаимоиндукцией, аналогично сопротивлению, обусловленному самоиндукцией, так как э. д. с. взаимоиндукции влияет на режим цепи с качественной стороны так же, как и э. д. с. самоиндукции.

Одноименные и разноименные зажимы индуктивно-связанных катушек
Ранее было дано определение согласного и встречного включения катушек.
При согласном включении магнитные потоки самоиндукции и взаимоиндукции в обеих катушках по направлению совпадают, поэтому э. д. с. самоиндукции и взаимоиндукции в каждой катушке также направлены одинаково.

При встречном включении магнитные потоки, а также э. д. с. самоиндукции и взаимоиндукции по направлению противоположны.

На схемах замещения взаимная индуктивность обозначается буквой М и дугой, объединяющей два индуктивно-связанных элемента (рис. 16.1). Для того чтобы различать согласное и встречное включения, на схемах обозначают также начала индуктивно-связанных катушек, отмечая их точками или звездочками.
 

Зажимы индуктивно-связанных катушек называют одноименными (начала или концы), если при согласном включении положительное направление токов, принятое на схеме, относительно этих зажимов одинаково (рис. 16.1, а). При встречном включении (рис. 16.1, б) ток в одной катушке направлен к началу, а в другой — к концу.
 

Разметка зажимов на основе опыта

Направление магнитных потоков катушек зависит от их взаимного расположения и направления намотки витков. При отсутствии сведений о расположении начал и концов можно провести простой опыт, для которого кроме самих индуктивно-связанных катушек требуется гальванический элемент (или аккумулятор) и гальванометр (рис. 16.2).

Рис. 16.2. Схема опыта для разметки зажимов катушек

Одну из катушек через ключ присоединяют к гальваническому элементу, к зажимам другой подключают гальванометр. В момент замыкания ключа К возникают токи в обеих катушках, причем ток i₂ создает магнитный поток, направленный навстречу потоку первой катушки (правило Ленца). Поэтому при включении гальванического элемента токи i₁ и i₂ направлены противоположно относительно одноименных зажимов. Направление тока i₁ известно, так как известна полярность источника питания, а направление тока i₂ определяется по отклонению гальванометра.

Ток i₂ направлен к положительному зажиму гальванометра, если стрелка его отклоняется по шкале (шкала односторонняя).

Одноименными зажимами катушек являются зажимы, к которым присоединены положительные зажимы источника и гальванометра; другие два зажима также одноименны.