Что такое делитель напряжения и как его рассчитать?

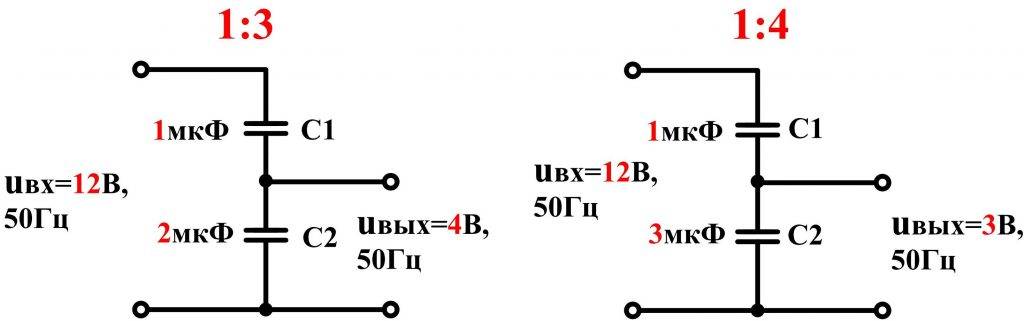
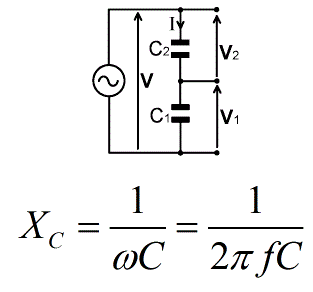Делитель напряжения на резисторах

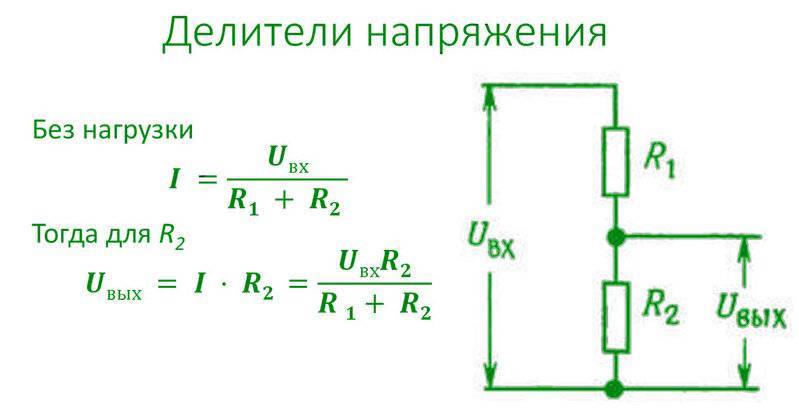
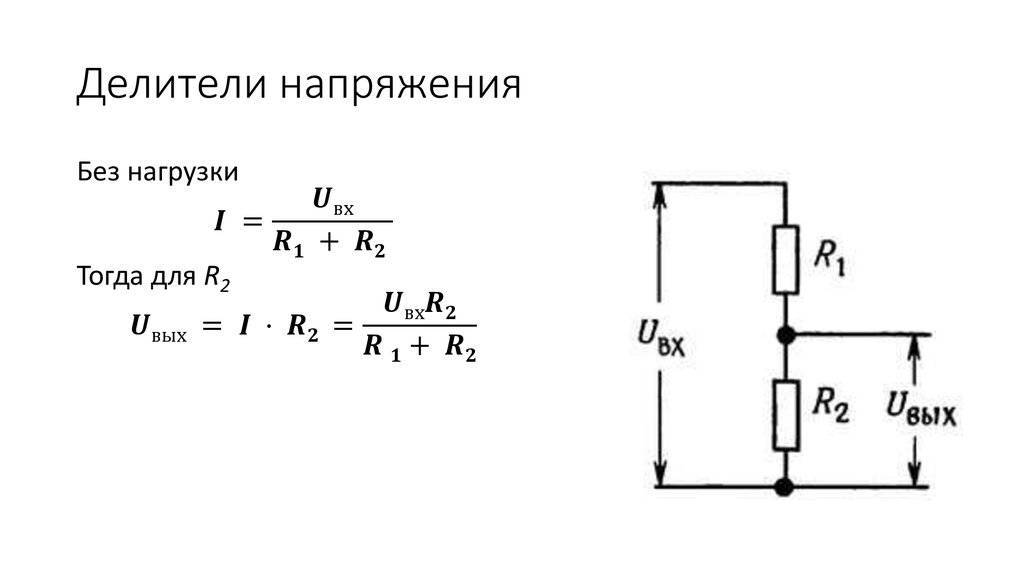
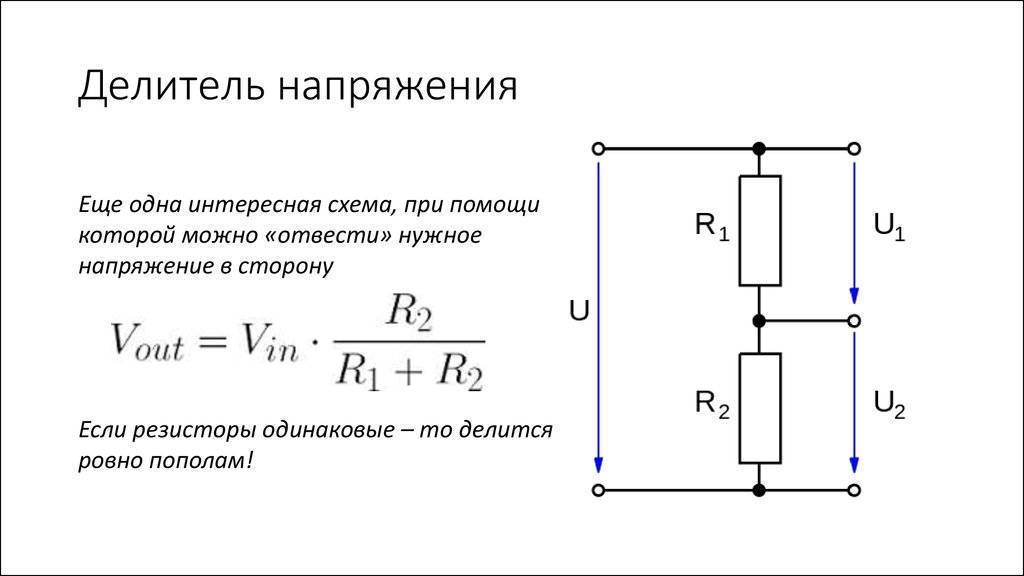
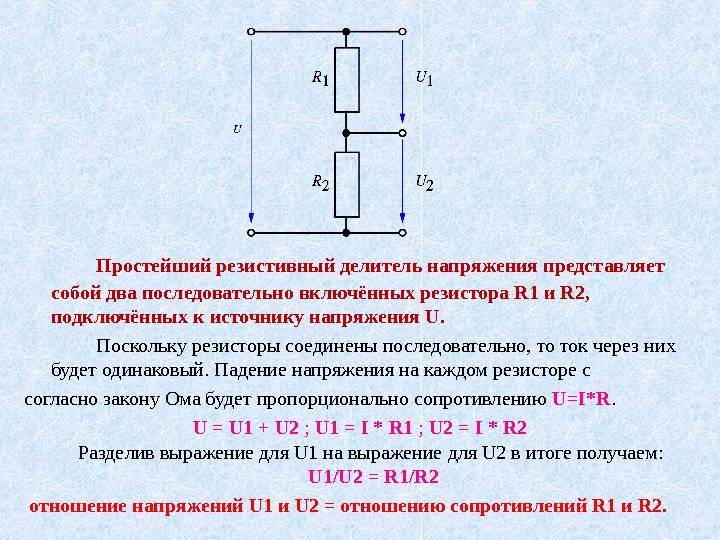
Давайте разберем самый простой делитель напряжения, состоящий из двух резисторов. Эти два резистора соединим последовательно и подадим на них напряжение. Напряжение может быть как постоянное, так и переменное.

Подавая напряжение на эту цепь, состоящую из двух резисторов, у нас получается, что цепь становится замкнутой, и в цепи начинает течь электрический ток с какой-то определенной силой тока, которая зависит от номиналов резисторов.

Итак, мы знаем, что при последовательном соединении сила тока в цепи одинакова. То есть какая сила тока протекает через резистор R1, такая же сила тока течет и через резистор R2. Как же вычислить эту силу тока? Оказывается, достаточно просто, используя закон Ома: I=U/R.

Так как наши резисторы соединены последовательно, то и их общее сопротивление будет выражаться формулой

То есть в нашем случае мы можем записать, что

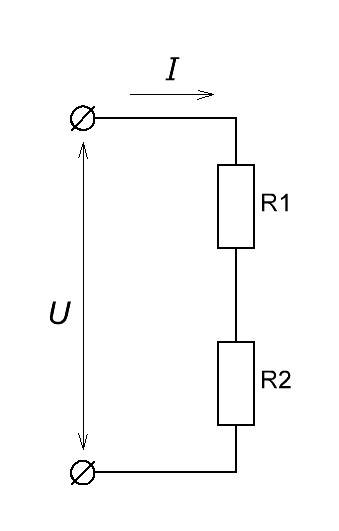
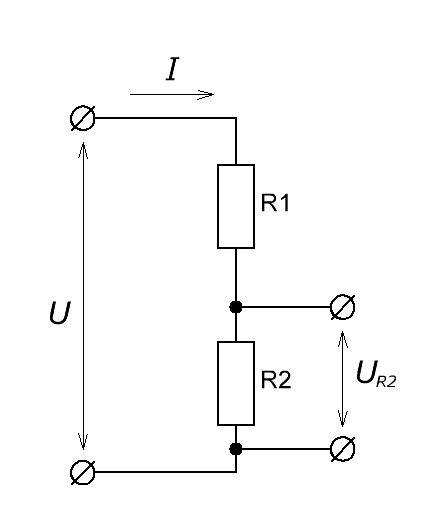
Как найти напряжение, которое падает на резисторе R2?

Так как ток для обоих резисторов общий, то согласно закону Ома

Подставляем вместо I формулу

и получаем в итоге

Для другого резистора ситуация аналогичная. На нем падает напряжение

Для него формула запишется

Давайте докажем, что сумма падений напряжений на резисторах равняется напряжению питания, то есть нам надо доказать, что U=U_R1 +U_R2 . Подставляем значения и смотрим.

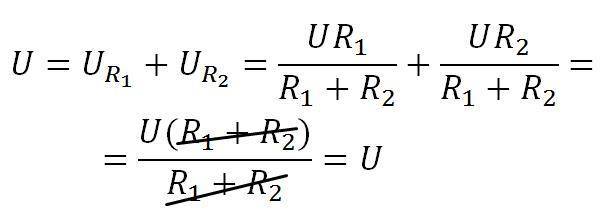
что и требовалось доказать.

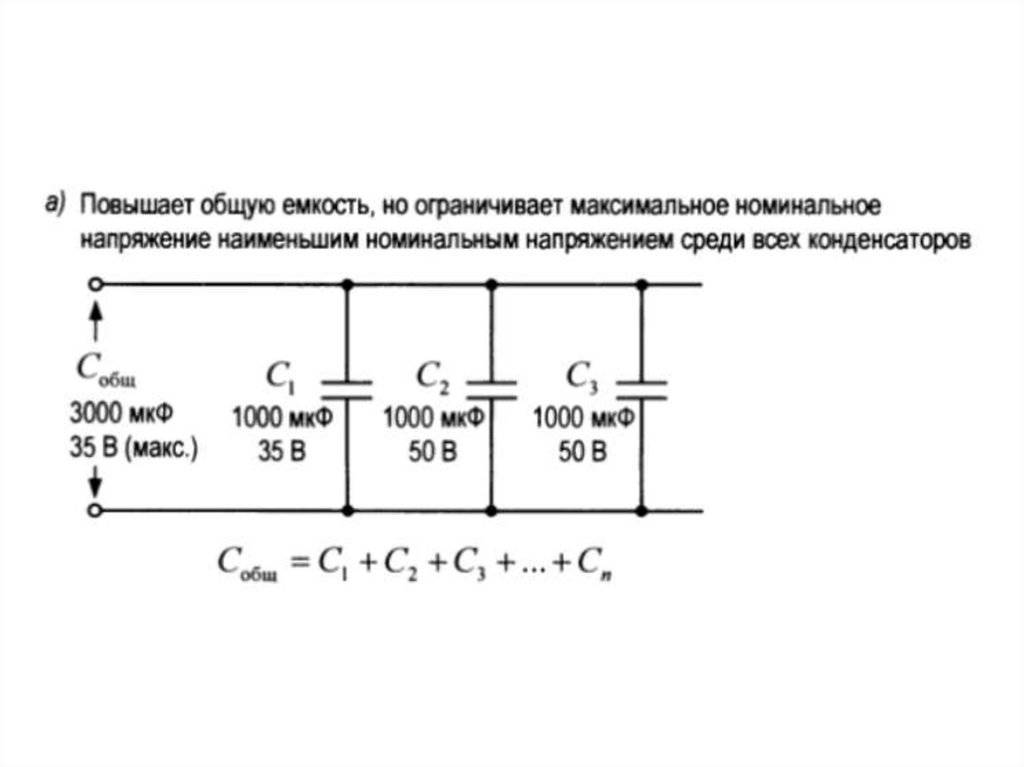
Эта формула также работает и для большого количества резисторов.

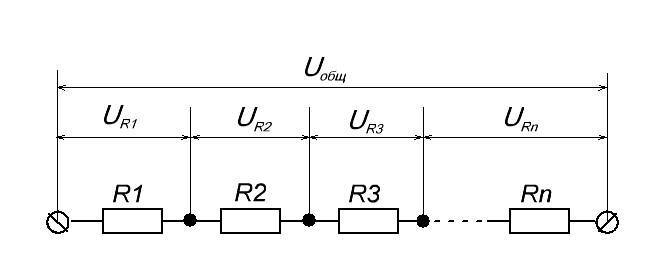
На схеме выше мы видим резисторы, которые соединены последовательно. Чему будет равняться U_общ ? Так как резисторы соединены последовательно, следовательно, на каждом резисторе падает какое-то напряжение. Сумма падений напряжения на всех резисторах будет равняться U_общ . В нашем случае формула запишется как

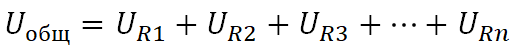
Применение

Использование такой схемотехники на практике демонстрируют следующие примеры. Для расчетов электрических параметров без учета сопротивления нагрузки подойдут рассмотренные выше ручные и автоматизированные методики.

Потенциометры

Если резистор оснастить ползунком и соответствующим приводом, сопротивления можно будет менять плавно. Это решение позволяет точнее менять напряжения на выходе, по сравнению с дискретными схемами. Главный недостаток – усложнение конструкции, что, кроме удорожания, снижает надежность. Приходится обеспечивать герметичность рабочей зоны для исключения загрязнения и предотвращения коррозийных процессов.

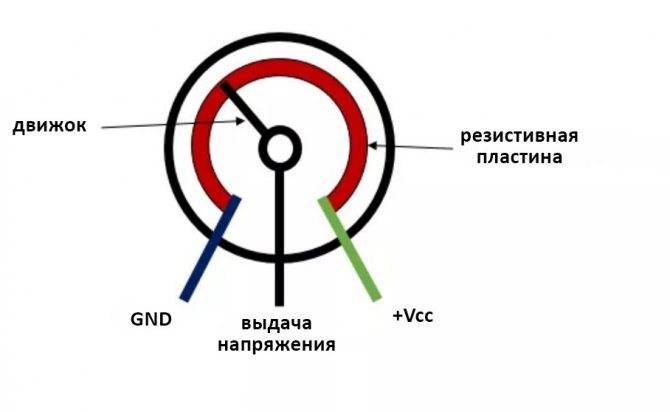
Принципиальная схема потенциометра

Резистивные датчики

В этом варианте пользуются способностью некоторых материалов увеличивать/ уменьшать электрическое сопротивление под воздействием температуры, светового потока, других внешних воздействий. Созданный на основе этих принципов датчик устанавливают в плечо делителя. По уровню напряжения на выходе контролируют изменение соответствующих параметров.

Цепи обратной связи в усилителях

Таким решением обеспечивают необходимый коэффициент усиления. На представленной ниже схеме этот параметр не будет никогда ниже единицы. Для повышения уровня преобразования увеличивают значение сопротивления R2 по отношению к R1.

Делитель напряжения в цепи обратной связи

Простейшие электрические фильтры

Для фильтрации заменяют конденсатором резисторы R1 или R2. В первом варианте устройство беспрепятственно пропускает высокочастотные составляющие. При снижении частоты до определенного уровня реактивное сопротивление увеличивается, препятствует прохождению тока. Аналогичным образом делают изменения в нижнем плече делителя с целью отсечения низких частот.

Усилитель напряжения

Переменным резистором изменяют уровень сигнала для получения необходимой громкости звучания. В таких устройствах применяют элементы с логарифмической характеристикой изменения сопротивления, что хорошо соответствует естественному механизму восприятия человеческими органами слуха.

Параметрический стабилизатор напряжения

В таких схемах нижнее плечо делителя можно создать с применением стабилитрона. Его вольтамперные характеристики выбирают таким образом, чтобы выходное напряжение сохраняло нужное значение при изменении входных параметров.

Примеры небольших потенциометров

Ниже показано несколько небольших потенциометров, которые обычно используются в бытовом электронном оборудовании, а также любителями и студентами при построении схем:

Рисунок 17 – Примеры небольших потенциометров

Меньшие устройства слева и справа предназначены для подключения к беспаечной макетной плате или для пайки в печатную плату. Устройства посередине предназначены для установки на плоской панели с проводами, припаянными к каждому из трех выводов.

Ниже показано еще три потенциометра, более специализированных, чем только что показанный набор:

Рисунок 18 – Примеры потенциометров размером побольше

Большое устройство «Helipot» – это лабораторный потенциометр, предназначенный для быстрого и легкого подключения к цепи. Устройство в нижнем левом углу фотографии представляет собой потенциометр того же типа, только без корпуса и поворотного счетного диска. Оба этих потенциометра представляют собой прецизионные устройства, в которых используются многооборотные спиралевидные резистивные ленты и ползунковые механизмы для точной регулировки. Устройство в правом нижнем углу представляет собой потенциометр для монтажа на панели, предназначенный для работы в тяжелых промышленных условиях.

Примеры

Резистивный делитель

Рисунок 2: Простой резистивный делитель напряжения

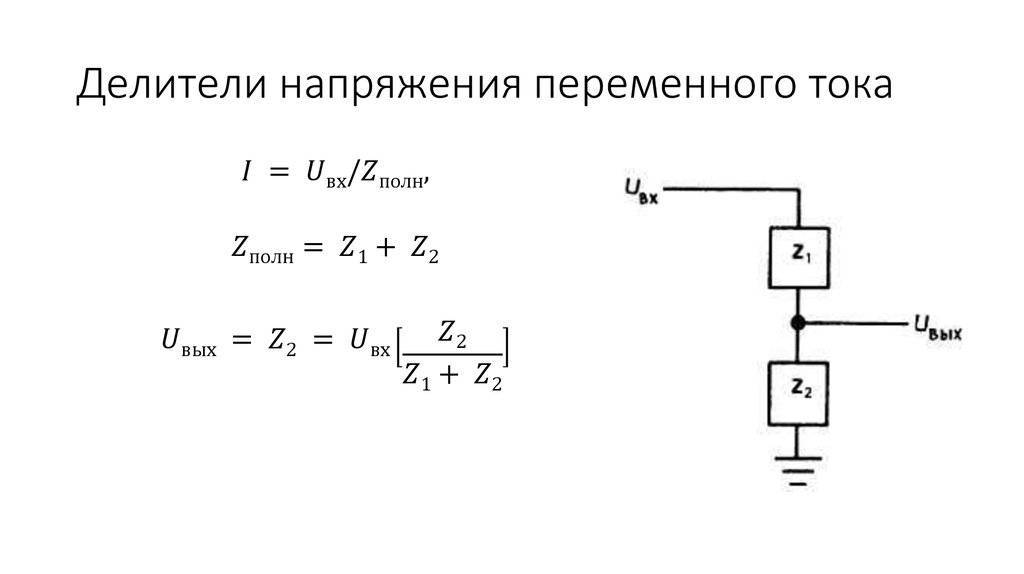
Резистивный делитель – это случай, когда оба импеданса Z₁ и Z₂, являются чисто резистивными (рис. 2).

Подставляя Z₁ = R₁ и Z₂ = R₂ в предыдущее выражение дает:

Vотыт=р2р1+р2⋅Vяп{ Displaystyle V _ { mathrm {out}} = { frac {R_ {2}} {R_ {1} + R_ {2}}} cdot V _ { mathrm {in}}}

Если р₁ = р₂ тогда

Vотыт=12⋅Vяп{ Displaystyle V _ { mathrm {out}} = { frac {1} {2}} cdot V _ { mathrm {in}}}

Если V_из = 6В и V_в = 9 В (оба обычно используются напряжения), тогда:

VотытVяп=р2р1+р2=69=23{ displaystyle { frac {V _ { mathrm {out}}} {V _ { mathrm {in}}}} = { frac {R_ {2}} {R_ {1} + R_ {2}}} = { frac {6} {9}} = { frac {2} {3}}}

и решая с помощью алгебра, р₂ должно быть вдвое больше р₁.

Чтобы решить для R1:

р1=р2⋅VяпVотыт−р2=р2⋅(VяпVотыт−1){ displaystyle R_ {1} = { frac {R_ {2} cdot V _ { mathrm {in}}} {V _ { mathrm {out}}}} – R_ {2} = R_ {2} cdot left ({{ frac {V _ { mathrm {in}}} {V _ { mathrm {out}}}} – 1} right)}

Чтобы решить для R2:

р2=р1⋅1(VяпVотыт−1){ Displaystyle R_ {2} = R_ {1} cdot { frac {1} { left ({{ frac {V _ { mathrm {in}}} {V _ { mathrm {out}}}} – 1} right)}}}

Любое соотношение V_из/V_в больше 1 невозможно. То есть с помощью одних только резисторов невозможно ни инвертировать напряжение, ни увеличить V_из над V_в.

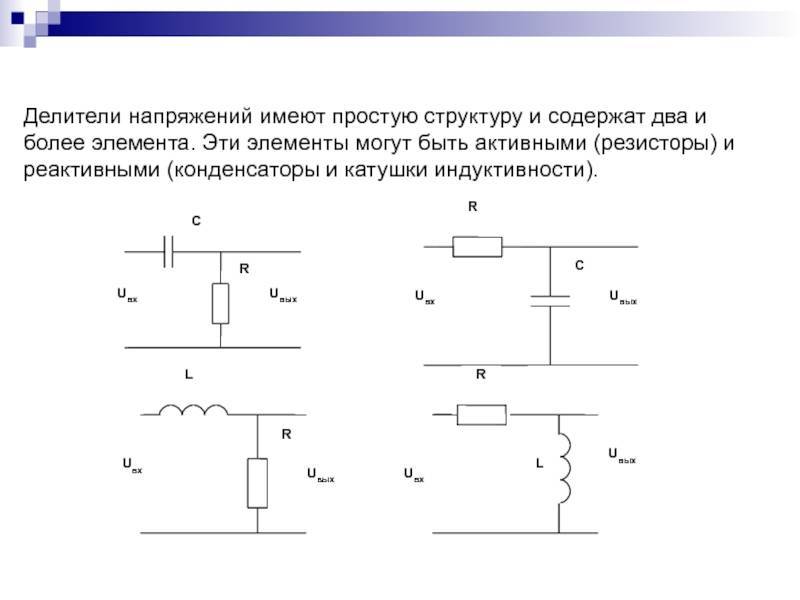
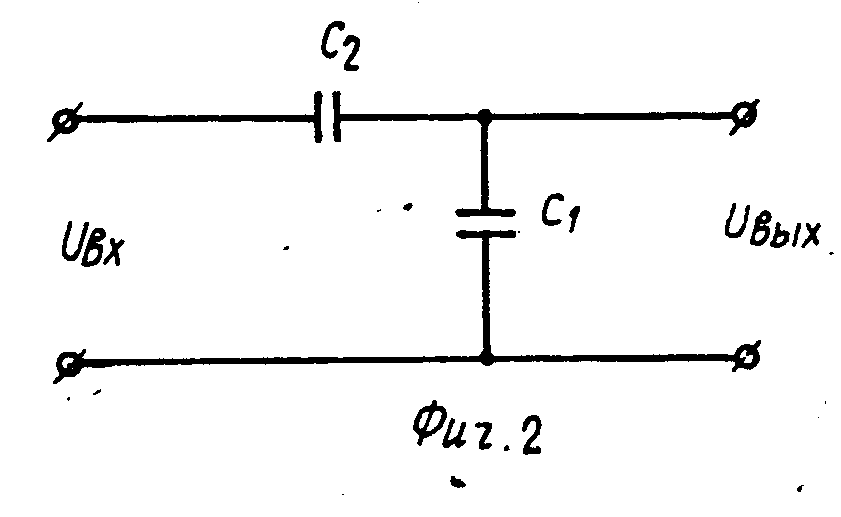
RC фильтр нижних частот

Рисунок 3: Резисторный / конденсаторный делитель напряжения

Рассмотрим делитель, состоящий из резистора и конденсатор как показано на рисунке 3.

Сравнивая с общим случаем, мы видим Z₁ = R и Z₂ импеданс конденсатора, определяемый

Z2=−jИксC=1jωC ,{ Displaystyle Z_ {2} = – mathrm {j} X _ { mathrm {C}} = { frac {1} { mathrm {j} omega C}} ,}

где X_C это реактивное сопротивление конденсатора, C – емкость конденсатора, j это мнимая единица, и ω (омега) это радианная частота входного напряжения.

Тогда этот делитель будет иметь соотношение напряжений:

VотытVяп=Z2Z1+Z2=1jωC1jωC+р=11+jωрC .{ displaystyle { frac {V _ { mathrm {out}}} {V _ { mathrm {in}}}} = { frac {Z _ { mathrm {2}}} {Z _ { mathrm {1}} + Z _ { mathrm {2}}}} = { frac { frac {1} { mathrm {j} omega C}} {{ frac {1} { mathrm {j} omega C}} + R}} = { frac {1} {1+ mathrm {j} omega RC}} .}

Продукт τ (тау) = RC называется постоянная времени схемы.

Соотношение затем зависит от частоты, в этом случае уменьшается с увеличением частоты. Эта схема, по сути, является базовой (первого порядка) фильтр нижних частот. Отношение содержит мнимое число и фактически содержит как амплитуду, так и сдвиг фазы информация о фильтре. Чтобы извлечь только отношение амплитуд, вычислите величина отношения, то есть:

|VотытVяп|=11+(ωрC)2 .{ displaystyle left | { frac {V _ { mathrm {out}}} {V _ { mathrm {in}}}} right | = { frac {1} { sqrt {1 + ( omega RC ) ^ {2}}}} .}

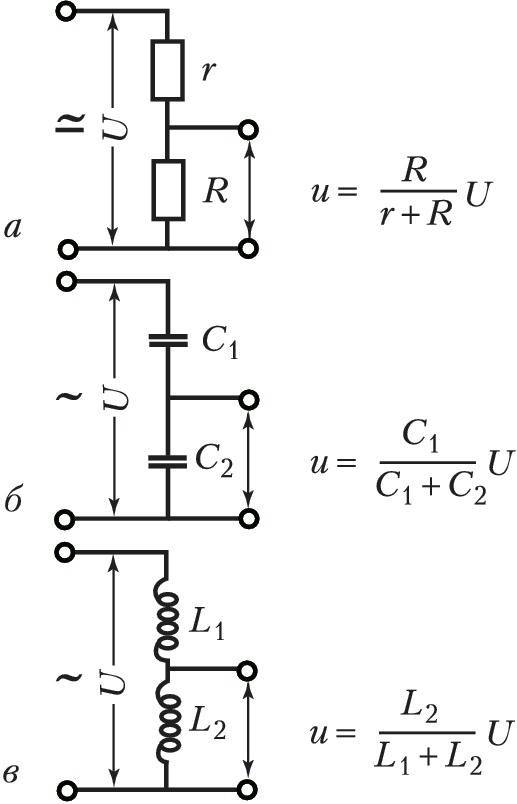
Индуктивный делитель

Индуктивные делители разделяют вход переменного тока по индуктивности:

Vотыт=L2L1+L2⋅Vяп{ displaystyle V _ { mathrm {out}} = { frac {L_ {2}} {L_ {1} + L_ {2}}} cdot V _ { mathrm {in}}}

Вышеприведенное уравнение предназначено для невзаимодействующих катушек индуктивности; взаимная индуктивность (как в автотрансформатор) изменит результаты.

Индуктивные делители делят вход постоянного тока в соответствии с сопротивлением элементов, как и в случае резистивного делителя, указанного выше.

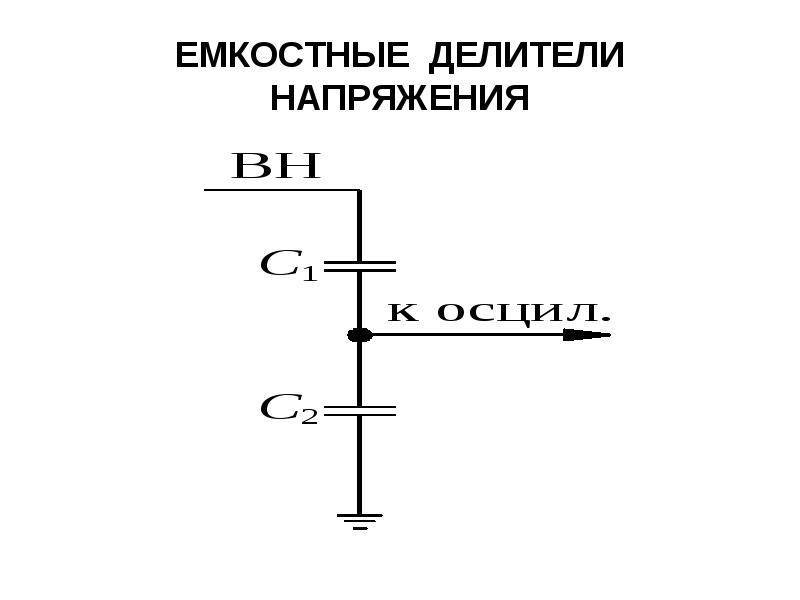
Емкостной делитель

Емкостные делители не пропускают вход постоянного тока.

Для входа переменного тока простое емкостное уравнение:

Vотыт=C1C1+C2⋅Vяп{ Displaystyle V _ { mathrm {out}} = { frac {C_ {1}} {C_ {1} + C_ {2}}} cdot V _ { mathrm {in}}}

Любой ток утечки в емкостных элементах требует использования обобщенного выражения с двумя импедансами. Путем выбора параллельных элементов R и C в надлежащих пропорциях можно поддерживать одинаковый коэффициент деления в полезном диапазоне частот. Это принцип, применяемый в компенсированных осциллограф зонды для увеличения ширины полосы измерения.

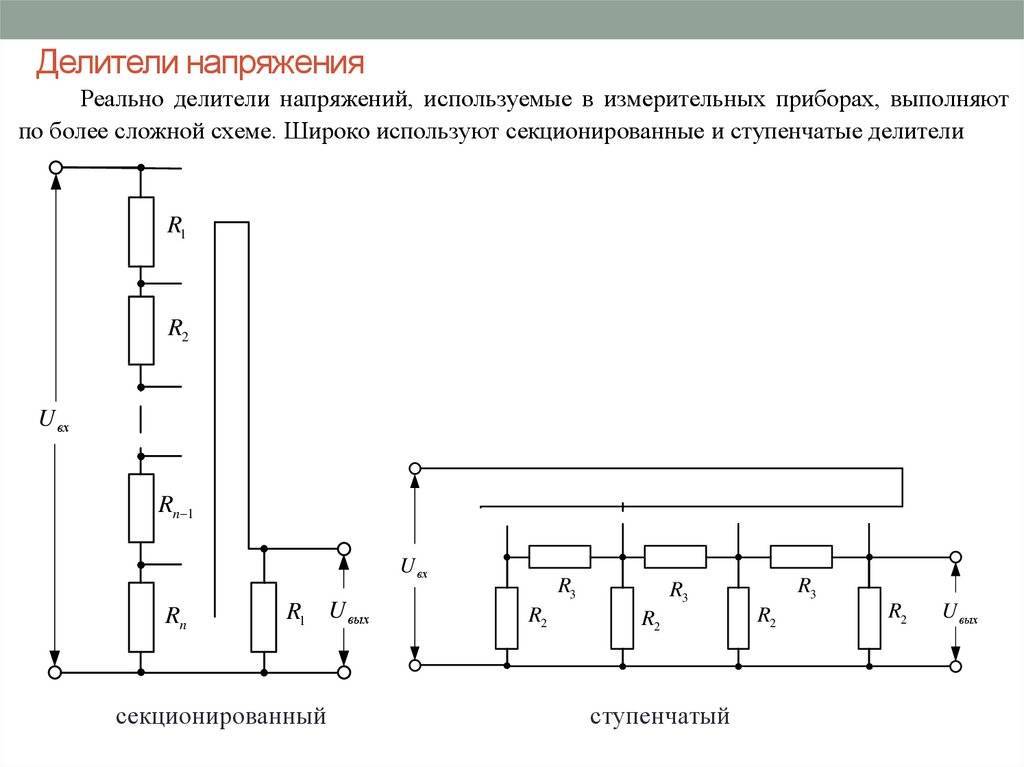
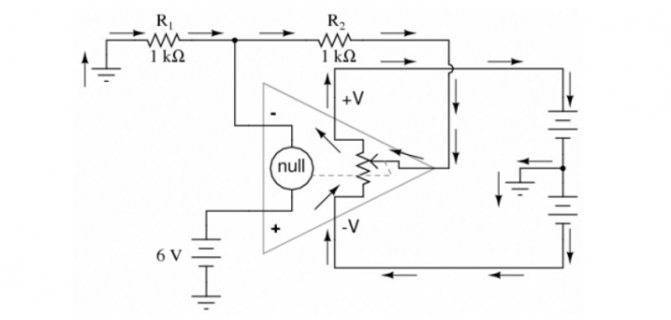
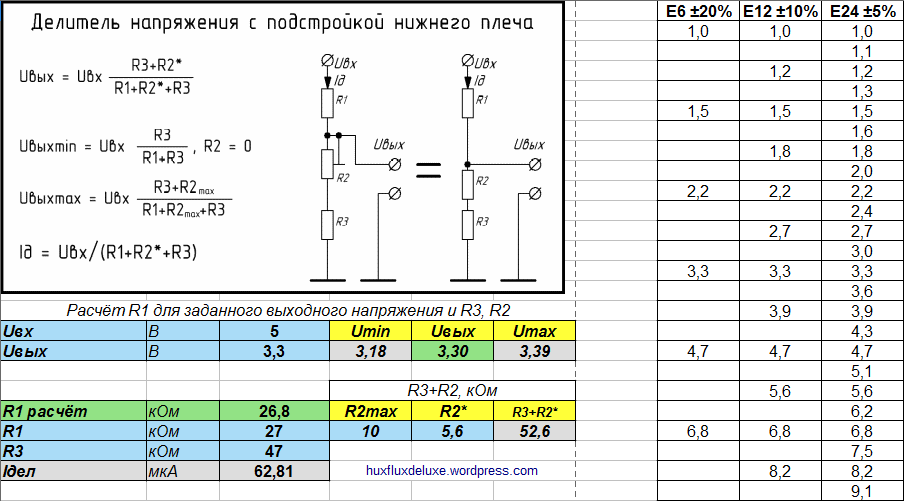
«Сложный» делитель (подбор сопротивления, расчёт напряжений)

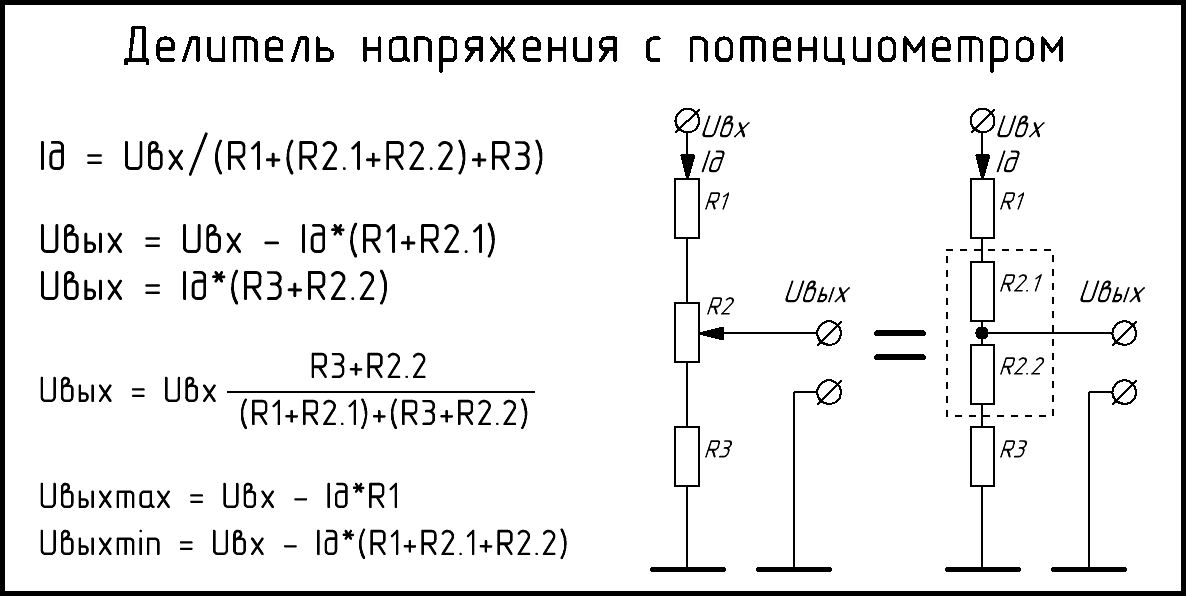
На первый взгляд эта разновидность делителя кажется сложной, а формулы и вовсе отпугивают. Однако подстроечный резистор, включённый по схеме потенциометра, делает схему очень предсказуемой. Сопротивление R2 всегда постоянно, поэтому ток делителя не меняется, и высчитать диапазон регулировки напряжения очень просто.

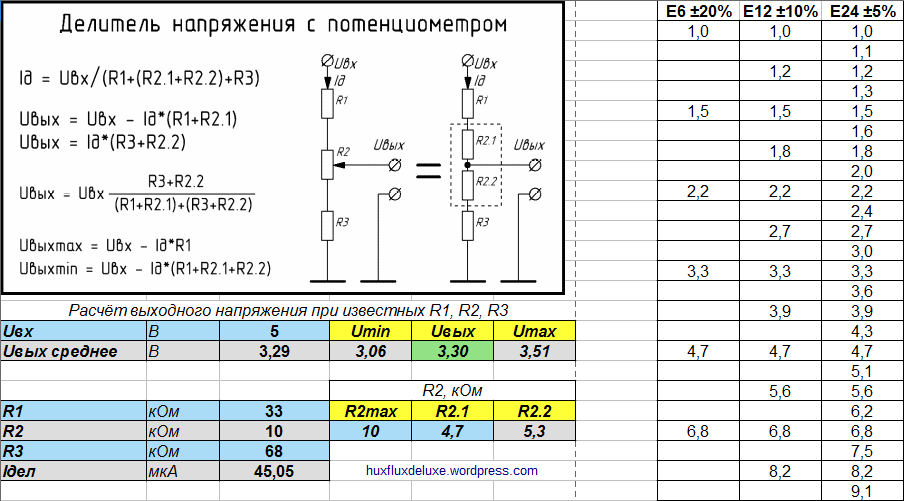
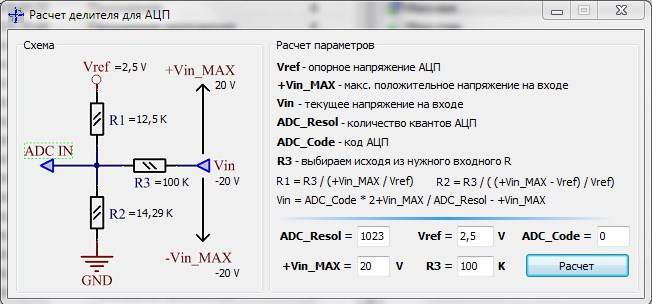
Калькулятор построен так, что после расчётов можно распечатать его страницу со всеми результатами. Если вдруг понадобится пересчитать делитель — есть формулы на картинке. Справа висит таблица стандартных номиналов радиодеталей — чтобы вы не кошмарили магазины мифическими резисторами на 77 кОм.Инструкция: 1. Задать входное напряжение Uвх. 2. Установить R2max и R2.1 в нули. R2.2 обнулится автоматически. 3. Подобрать такие R1 и R3, чтобы Uвых среднее было близким к нужному. 4. Для точной регулировки укажите максимальное сопротивление подстроечного резистора R2max. 5. Калькулятор выдаст диапазон регулировки (Umin, Umax) и текущее значение Uвых. Последнее можно менять, увеличив сопротивление R2.1. 6. В реальную схему вместо потенциометра можно поставить постоянные R2.1 и R2.2 рассчитанных номиналов.

Ещё калькулятор умеет считать напряжение самого простого двухрезисторного делителя. Для этого надо указать значения R1 и R3 при R2max и R2.1 = 0.

Замечание вообще про любые делители напряжения: Ток делителя Iдел должен быть в 10 и более раз больше, чем ток нагрузки. Иначе её сопротивление войдёт в состав R3, R2.2 и собьёт настройку. Поэтому делители используются там, где токи небольшие — до нескольких десятков миллиампер. Если же вы надумали сделать автомобильную зарядку для телефона через делитель — вы погорячились. И резисторы ваши тоже очень быстро разгорячатся на десяти амперах. Не надо так.

Параллельное и последовательное соединение резисторов, решение задач

Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно. Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. На схеме присутствует параллельная и последовательная часть соединения элементов

Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?

Будет интересно Как прочитать обозначение (маркировку) резисторов

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.

Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше. Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом

Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех. Заменяем эти сопротивление одним эквивалентным R23465

В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.

Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно. На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.

Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

• Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
• Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.

Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Типы подключений.

Что такое делитель тока

Какие ассоциации у вас возникают при словосочетании “делитель тока”? У меня сразу возникает ассоциация с делителем потока. Давайте представим себе реку, у которой очень большой поток.

Это поток воды бежит с очень большой скоростью! Он смывает на своем пути камни, землю, деревья. Представьте, что эта река находится рядом с вашим домом. Через год-два ваш дом смоет под чистую! Чтобы этого не произошло, надо ослабить течение реки, чтобы ее поток был слабый. Например как здесь:

Но как это сделать? А почему бы нам не прорыть большой канал, чтобы бОльшая часть воды текла через него. А это хорошая идея не так ли?

Весь смак заключается в том, что в каждой отдельной речке скорость воды будет меньше. В электротехнике и электронике все тоже самое! Река – это провод, сила потока – это сила тока, ширина реки – сопротивление, напряжение – угол наклона реки. Все элементарно и просто!

схема и расчёт [Амперка / Вики]

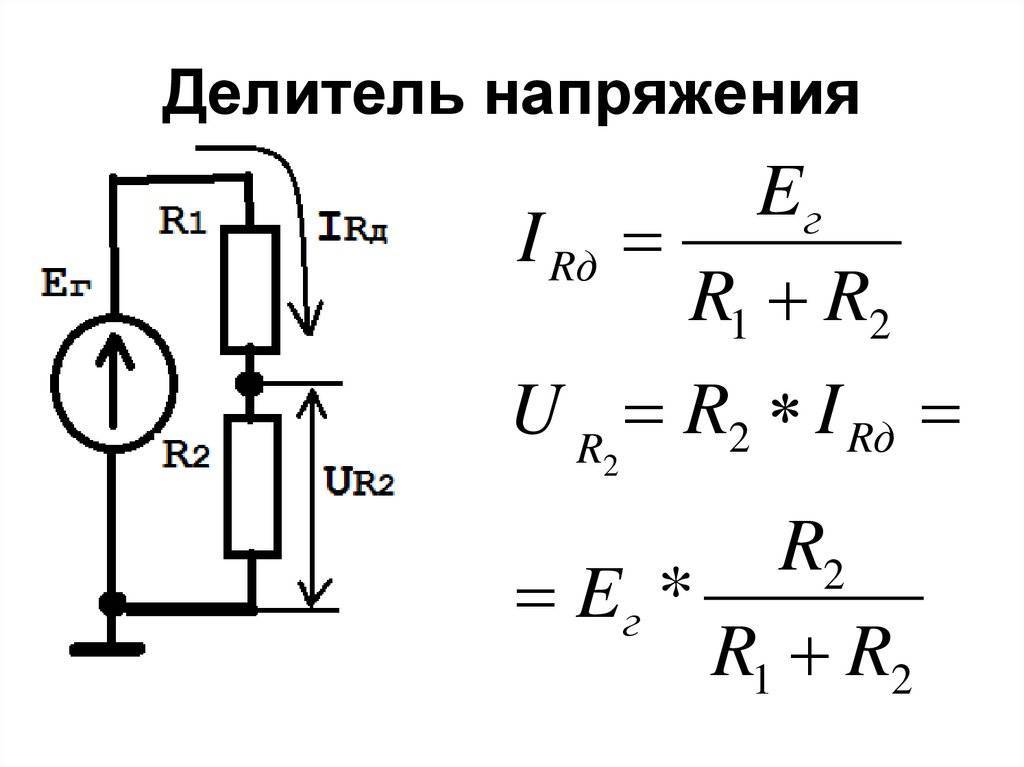
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов.

В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе Vout? Или эквивалентный вопрос: какое напряжение покажет вольтметр?

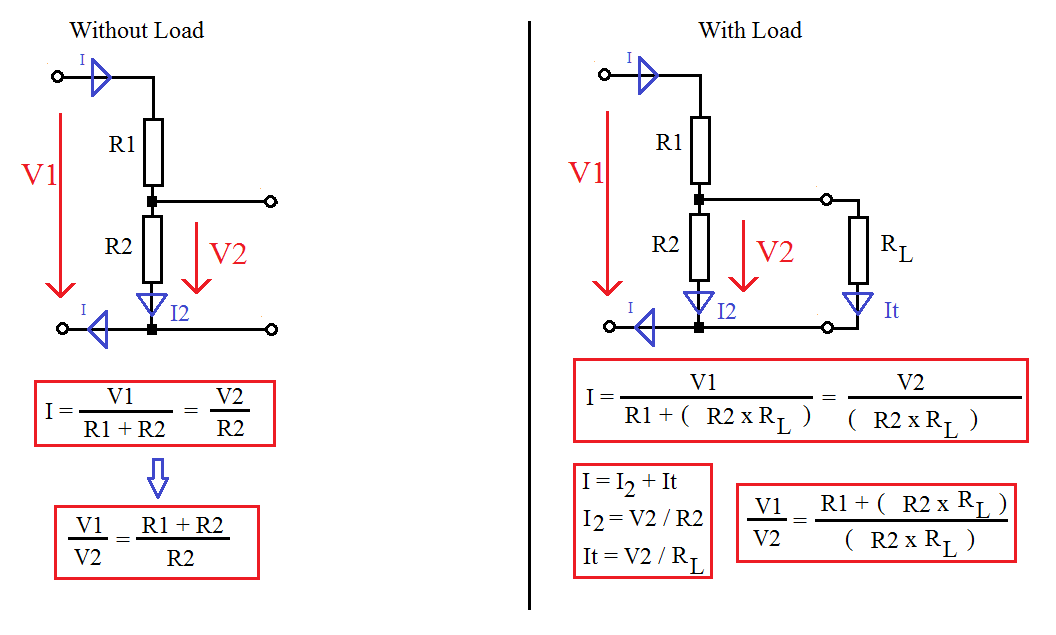
Ток, протекающий через R1 и R2 одинаков пока к выходу Vout ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:

Таким образом, сила тока протекающая через резисторы

Теперь, когда нам известен ток в R2, расчитаем напряжение вокруг него:

Или если отавить формулу в общем виде:

Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при этом только один источник питания.

Применение делителя для считывания показаний датчика

Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество компонентов, которые меняют своё сопротивление в зависимости от внешних условий. Так термисторы меняют сопротивление от нуля до определённого значения в зависимости от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего на них света и т.д.

Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, Vout будет меняться в зависимости от внешних условий, влияющих на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды.

Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию на переменный компонент и общую формулу расчёта Vout.

Подключение нагрузки

С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):

В этом случае Vout уже не может быть расчитано лишь на основе значений Vin,

R1 и R2: сама нагрузка провоцирует дополнительное падение напряжения (voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда её сопротивление

В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:

Подставив значение в общую формулу расчёта Vout, получим:

Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L. Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.

Пропорция сохраняется, Vout не меняется:

А потери уменьшатся:

Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.

Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на R1 равна:

А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.

Применимость

Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора.

Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.

Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое самой нагрузкой.

Если потребление тока нагрузкой неравномерно во времени, Vout также будет неравномерным.

wiki.amperka.ru

Расчетные формулы

Допустим, есть схема с двумя резисторами. Расчет делителя напряжения на резисторах сводится к применению математических формул закона Ома и закона Кирхгофа.

1. Из закона Ома:

U = I x R, тогда U1 = I x R1, а U2 = I x R2,

где U – входное напряжение;

1. Применяя закон Кирхгофа о том, что алгебраическая сумма напряжений вокруг замкнутого контура равна нулю, можно записать следующие формулы:

U = U1 + U2, следовательно, U = U1 + U2;

1. Поэтому U = I x R1 + I x R2, отсюда I = U/(R1 + R2);
2. Если подставить полученные выводы в формульную запись закона Ома, то получится падение напряжения на отдельных резисторных элементах:

U1 = R1 x U/(R1 + R2) и U2 = R2 x U/(R1 + R2).

Напряжение, распределенное на двух резисторах, пропорционально соотношению их сопротивлений. Это отношение не может быть больше 1 для любых значений R1 и R2, поэтому Uвх сокращается до Uвых с фиксированным соотношением, определяемым величинами R1 и R2.

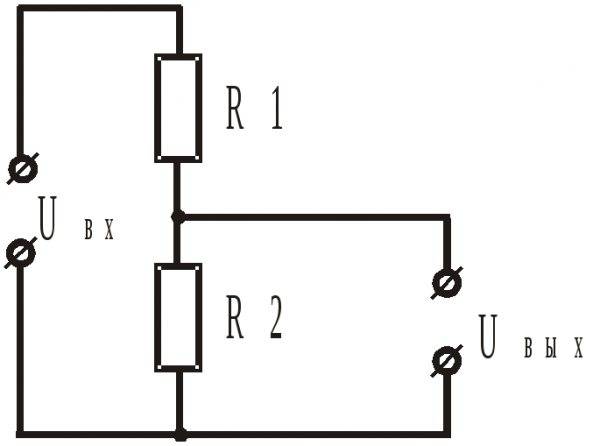
Расчетная схема делителя напряжения

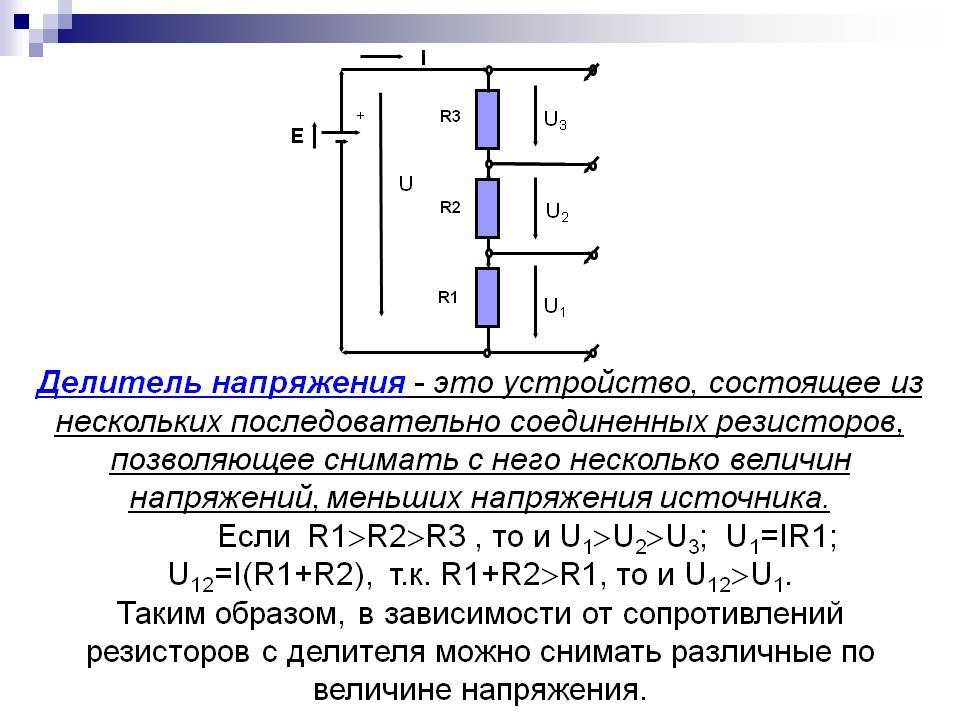
Важно! Это правило распространяется и на цепи, рассчитанные более, чем на два резистора. Например, U3 = R3 x U/(R1 + R2 + R3) и U4 = R4 x U/(R1 + R2 + R3 +R4)

Полученное соотношение – это формула делителя напряжения. Именно по ней выполняется расчет самостоятельно или в калькуляторе онлайн для делителя напряжения.

Если заданы величины напряжения выхода, то можно выполнить расчет резистора, используя данные формулы:

• R1 = U1 x R/U;
• R2 = (U2 x R/U) – R1;
• R3 = (U3 x R/U) – (R1 + R2) и т.д.

Калькулятор делителя напряжения

Разделитель напряжения представляет собой схему, используемую для создания напряжения, которое меньше или равно входному напряжению.

Как найти выходное напряжение цепи делителя

Два делителя напряжения резистора являются одной из наиболее распространенных и полезных схем, используемых инженерами. Основная цель этой схемы заключается в уменьшении входного напряжения до более низкого значения в зависимости от отношения двух резисторов. Этот калькулятор помогает определить выходное напряжение схемы делителя с учетом входного (или источника) напряжения и значений резисторов

Обратите внимание на то, что выходное напряжение в реальных схемах может быть различным, поскольку резистор и сопротивление нагрузки (при подключении выходного напряжения) становятся факторами

Уравнение

$$ V_ $$ = Выходное напряжение. Это уменьшенное напряжение.

$$ V_ $$ = Входное напряжение.

$$ R_ $$ и $$ R_ $$ = значения резистора. Отношение $$ frac > + R_ > $$ определяет масштабный коэффициент.

Приложения

Поскольку делители напряжения довольно распространены, их можно найти в ряде приложений. Ниже приведены лишь некоторые из мест, где эта схема найдена.

потенциометры

Возможно, наиболее распространенной схемой делителя напряжения является то, что используется потенциометр, который является переменным резистором. Схематическое изображение потенциометра показано ниже:

«Горшок» обычно имеет три внешних контакта: два являются концами резистора, а один подключен к рычагу стеклоочистителя. Стеклоочиститель разрезает резистор пополам и перемещает его, регулируя соотношение между верхней половиной и нижней половиной резистора. Соедините два внешних выводы к напряжению (вход) и ссылку (земля) со средним (стеклоочистители штифтом) в качестве выходного контакта и вы сам делитель напряжения.

Уровневые сдвиги

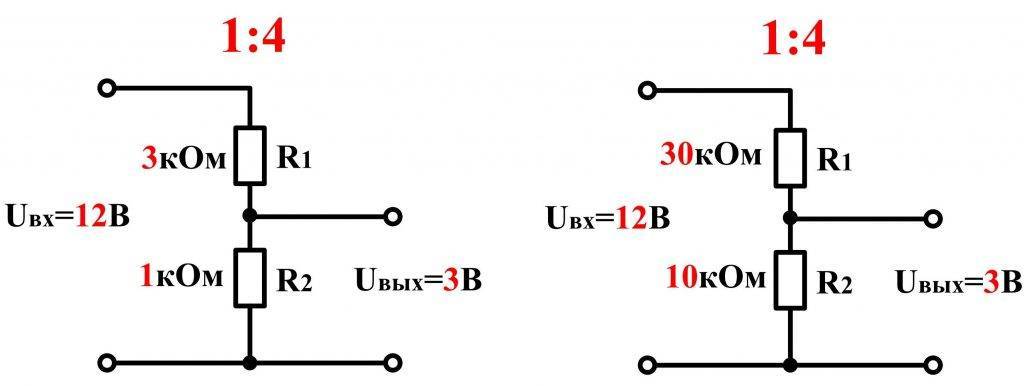
Другая область, в которой используются делители напряжения, – это когда напряжение должно быть выровнено. Наиболее распространенным сценарием является взаимодействие сигналов между датчиком и микроконтроллером с двумя разными уровнями напряжения. Большинство микроконтроллеров работают при напряжении 5 В, в то время как некоторые датчики могут принимать только максимальное напряжение 3, 3 В. Естественно, вы хотите выровнять напряжение от микроконтроллера, чтобы избежать повреждения датчика. Пример схемы показан ниже:

Схема выше показывает схему делителя напряжения, включающую резистор 2 кОм и 1 кОм. Если напряжение от микроконтроллера составляет 5 В, то пониженное напряжение на датчик рассчитывается как:

Этот уровень напряжения теперь безопасен для работы датчика

Обратите внимание, что эта схема работает только для выравнивания напряжений и не выравнивания

Ниже приведены некоторые другие комбинации резисторов, используемые для выравнивания часто встречающихся напряжений:

Комбинация резисторов	использование
4, 7 кОм и 6, 8 кОм	От 12 В до 5 В
4, 7 кОм и 3, 9 кОм	9V до 5V
3, 6 кОм и 9, 1 кОм	От 12 В до 3, 3 В
3, 3 кОм и 5, 7 кОм	От 9 В до 3, 3 В

Чтение резистивного датчика

Многие датчики являются резистивными устройствами и большинством микроконтроллеров считывают напряжение, а не сопротивление. Таким образом, резистивный датчик обычно подключается в цепи делителя напряжения с резистором для взаимодействия с микроконтроллером. Пример установки показан ниже:

Термистор – это датчик, сопротивление которого изменяется пропорционально температуре. Скажем, что термистор имеет сопротивление комнатной температуре 350 Ом. Сопряженное сопротивление выбирается равным 350 Ом.

Когда термистор находится при комнатной температуре, выходное напряжение:

Когда температура увеличивается, сопротивление термистора изменяется до 350, 03 Ом, выход изменяется на:

Такое небольшое изменение напряжения обнаруживается микроконтроллером. Если функция передачи термистора известна, теперь можно рассчитать эквивалентную температуру.

Дальнейшее чтение

Техническая статья – Разделители напряжения и тока: что это такое и что они делают

Учебник – Глава 6 – Цепи Divider и законы Кирхгофа

Учебник – Потенциометр в качестве делителя напряжения