Закон Ома для полной цепи и для участка цепи: варианты записи формулы, описание и объяснение

Законы Кирхгофа

Электрика любого помещения выполняется в виде замкнутых, рабочих электрических цепей. Два главных закона, которые определяют процессы в электрических сетях, являются законы Кирхгофа. Их два. Оба из них применяются и для постоянных и для переменных токов.

Первый закон Кирхгофа утверждает:

Суммарная величина токов направленная к узлу электрической сети равна суммарной величине токов направленных от узла.

В практике на основе первого закона Кирхгофа основана работа Устройств защитного отключения (УЗО). Работа УЗО заключается в отключении электропитания сети при возникновении токов утечки. При нормальном режиме работы суммарное значение тока, втекающая в электрическую сеть равна значению тока утекающему из нее. Если равенство токов нарушается, значит, в сети есть утечка. УЗО сконструировано и подключено таким образом, что при утечке тока УЗО его обнаруживает и размыкает питание электросети.

Второй закон Кирхгофа гласит:

Любой замкнутый контур переменной электрической сети имеет равные значения комплексных напряжений и ЭДС (электродвижущих сил) на всех пассивных элементах сети.

Примечание: Комплексное напряжение это значение напряжение в сети переменного тока.

Практическое применение можно пояснить на любой квартирной группе электропитания. Для пояснения рассмотрим квартиру.

Сколько бы групп электропитания в квартире не было, на любой розетке или светильнике напряжение в сети (при рабочем режиме) будет 220 вольт.

Еще один основной закон электрики нужно вспомнить.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга

Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя

Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

В общем, это наиболее распространенные варианты использования этих соединений.

Действие электродвижущих сил

Электродвижущая сила (ЭДС) является скалярной величиной, характеризующей работу не электрических сил, заставляющих производить разность потенциалов на выходе.

Дополнительная информация. Скалярная величина – это когда она может быть выражена только определённым значением. В отличие от векторной величины, которая определяется не только значением, но и направлением.

Используется ЭДС в генераторах, преобразующих какую либо работу А (джоуль) в электрическую. Для этого могут быть использованы такие виды энергии по их происхождению:

• Механическая индукционная. Вывод ЭДС возникает при пересечении проводником линий магнитного поля;
• Механическая пьезоэлектрическая. Возникновение ЭДС происходит при деформации некоторых веществ;
• Световая энергия. Здесь ЭДС появляется в полупроводниках при действии на них световых лучей;
• Термическая энергия. ЭДС образуется, когда контакты из разнородных проводников находятся под разными температурами;
• Химическая энергия. Возникновение ЭДС происходит вследствие химических реакций.

В зависимости от характера энергии и устройства генератора ЭДС может возникать как переменная, так и постоянная. Переменная может быть как синусоидальная (магнитные индукционные генераторы), так и импульсная (пьезозажигалки). Постоянную ЭДС преобразуют в основном из химической (элементы питания, аккумуляторы), световой (фотоэлементы) энергий и температуры (элементы Пельтье).

Генераторы тока

ЭДС образует на разноименных проводниках разность потенциалов. Если не соединять проводником клеммы, на которых имеется разность потенциалов, то тока в цепи не будет. Следовательно, никакой энергии не будет израсходовано. На клеммах будет оставаться разность потенциалов. Работу для поддержания этой разности совершать не надо.

Если к клеммам с разностью потенциалов подключить проводник с нагрузкой, то через него будет протекать электрический ток, выполняя работу в нагрузке. При этом разность потенциалов на клеммах будет стремиться к 0, что приведёт к падению тока до 0. Для поддержания разности потенциалов стабильной величиной необходимо, чтобы ЭДС получала энергию. Эта энергия затрачивает работу, равную той, которая совершается в нагрузке.

Советуем изучить Типы стабилизаторов напряжения

Ток, напряжение и сопротивление цепи: что это такое?

Ток, напряжение и сопротивления – это, пожалуй, самые главные понятия, используемые в законе Ома. Причем для их обозначения используются, как правило, следующие латинские буквы:

• R – величина сопротивления (измеряется в омах, Ом);
• U – величина напряжения (измеряется в вольтах, В);
• I – сила тока (единица измерения –амперы, А).

Чтобы все было ясно с этими понятиями из курса школьной физики, дадим небольшое пояснение.

Итак, начнем, пожалуй, с того, что поясним, что такое цепь. Электрическая цепь возникает тогда, когда образуется проводящий путь для электрического заряда. Причем заряд в ней перемещается постоянно. Этот процесс его непрерывного перемещения по проводникам, входящим в состав цепи, и называют током. Часто его сравнивают с потоком воды, которая течет в полой трубе.

Силу или своего рода «насос», заставляющий частиц-носителей заряда (то есть электроны) передвигаться по цепи, называют напряжением. Оно представляет собой определенный потенциал или меру потенциальной энергии. Причем этот потенциал всегда относителен и существует только между двумя различными точками.

Если мы упоминаем какую-то величину напряжения, действующего в электрической сети, то мы всегда понимаем под этим определенную потенциальную энергию. То есть ту энергию, которая заставляет перемещаться носителей заряда (электроны) из одной точки цепи в другую конкретную точку. Если конкретных точек не упоминать, то термин «напряжение» утрачивает свой смысл.

Проходя через проводники, ток, как правило, сталкивается с некоторым трением или, иначе говоря, противодействием своему движению. Данное противодействие получило название сопротивления.

Наглядное представление закона Ома для школьников

Итак, мы дали краткое объяснение основных понятий. Поэтому теперь вполне можно переходить и к основному вопросу нашей статьи.

Практическое использование

Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.Применяем закон к любому участку цепи

Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.Находим силу токаРассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:

• Напряжение – 220 В;
• R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

• R=0,2 МОм;
• U=400 В.

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).Вычисление напряженияДля решения мы также воспользуемся законом, составленным Омом. Итак задача:

• R=20 кОм;
• I=10 мА.

Преобразуем исходные данные:

• 20 кОм = 20000 Ом;
• 10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление.

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.

Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров.

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

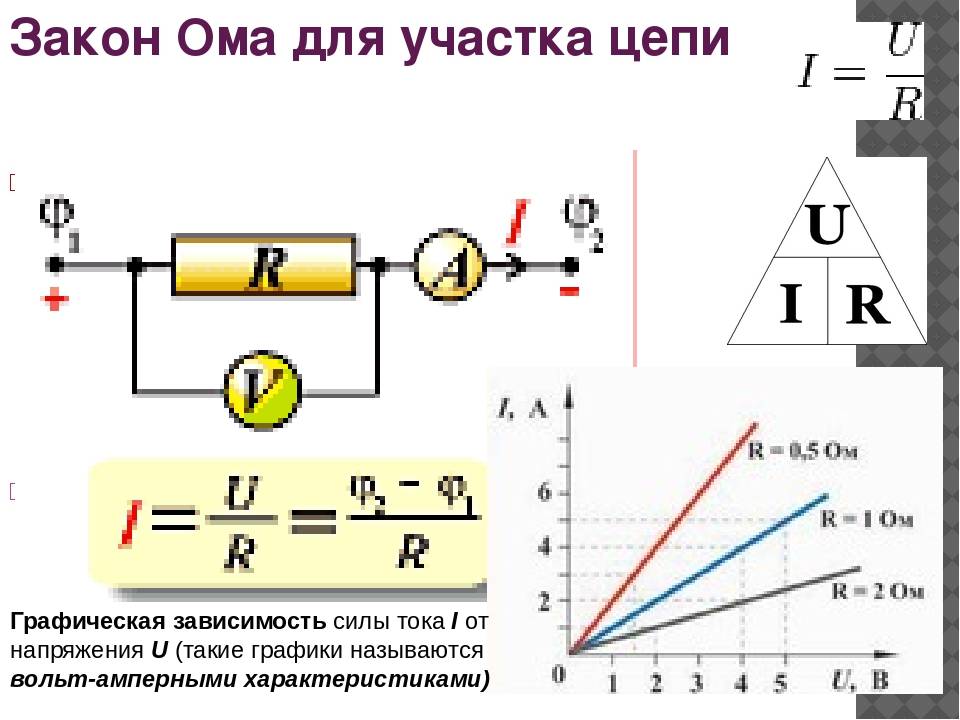
Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения

Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Источники

• https://poschitat.online/zakon-oma
• https://tel-spb.ru/ohm/
• https://www.fxyz.ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5/%D1%8D%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%BE/%D1%86%D0%B5%D0%BF%D0%B8_%D0%BF%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE_%D1%82%D0%BE%D0%BA%D0%B0/%D1%8D%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D1%81%D0%BE%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5/
• https://radioprog.ru/post/920
• https://elektroznatok.ru/info/teoriya/zakon-oma
• https://www.asutpp.ru/zakon-oma-dlya-uchastka-cepi.html

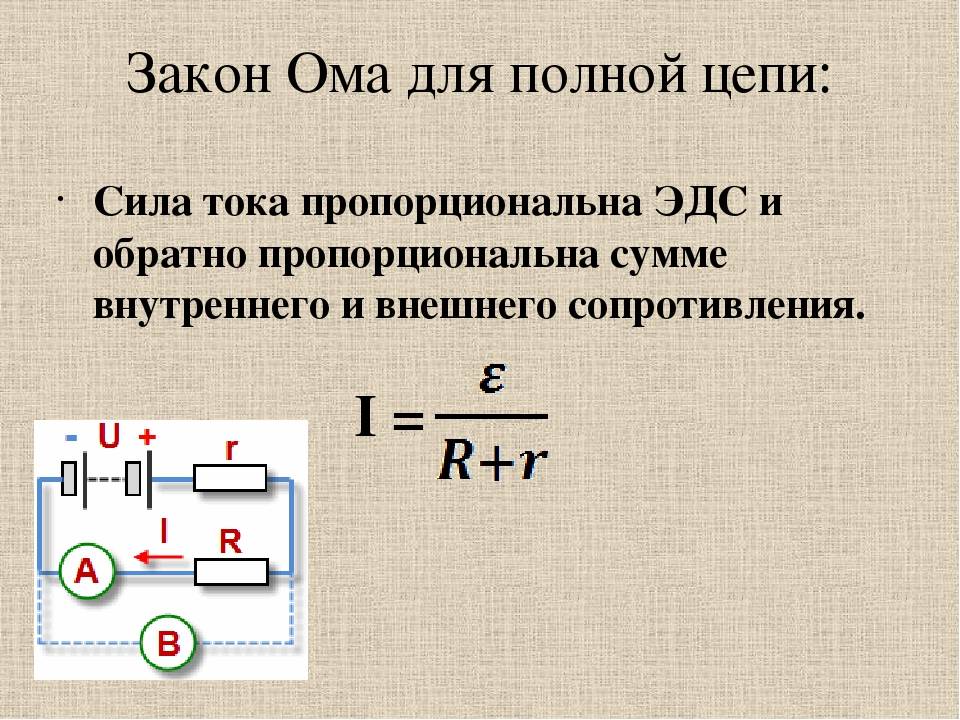
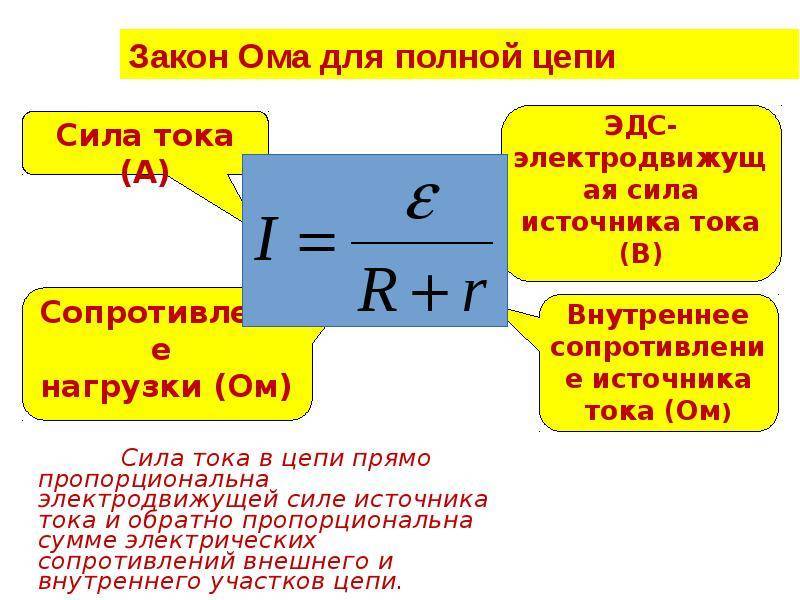
Закон Ома для полной цепи

Подробности

Просмотров: 522

«Физика – 10 класс»

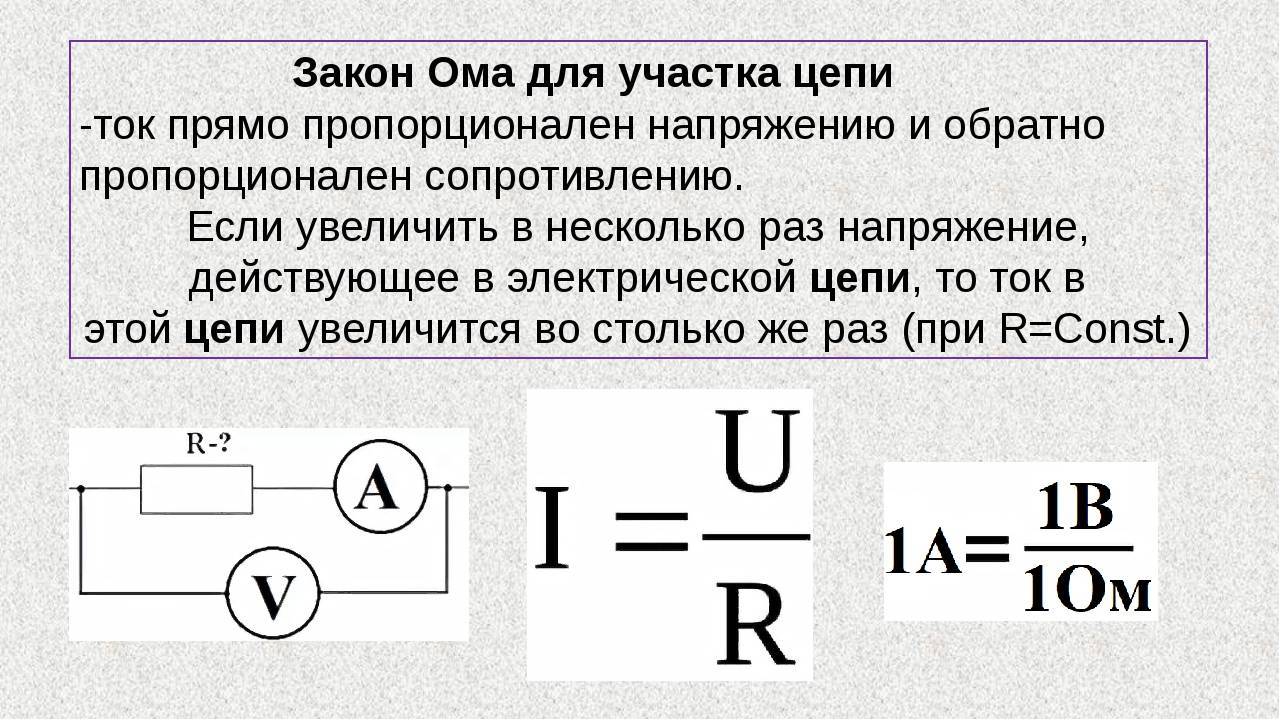
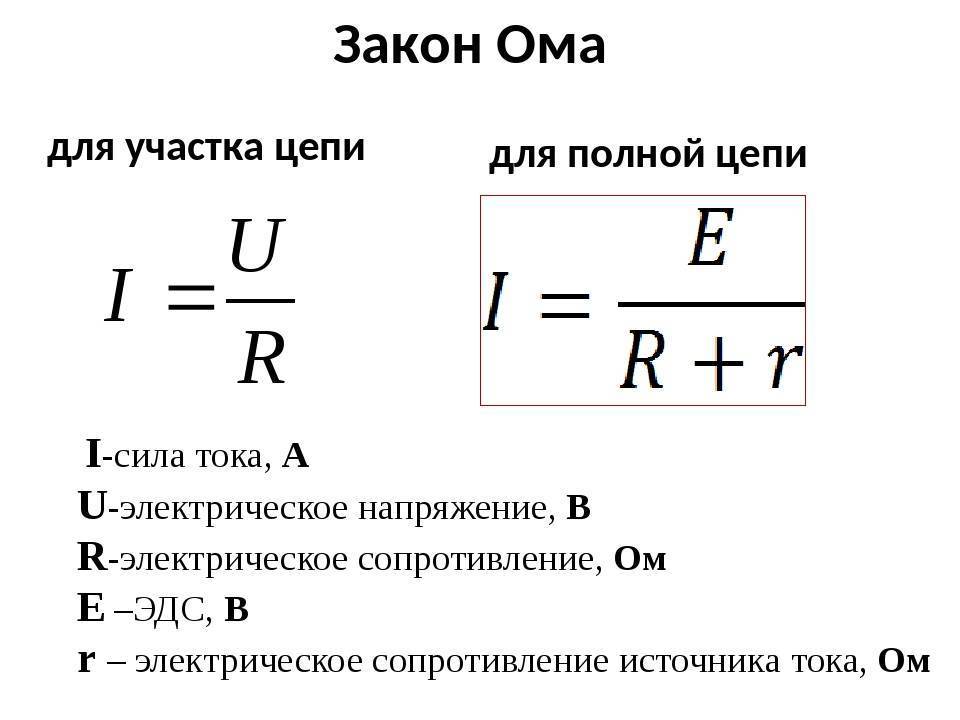
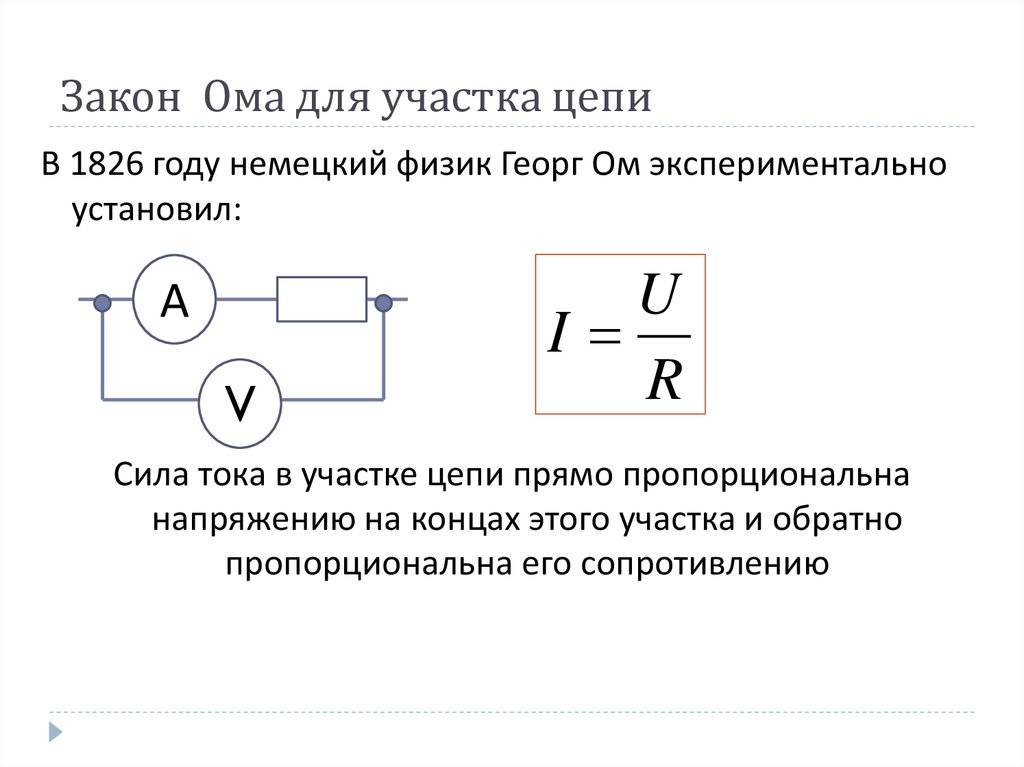
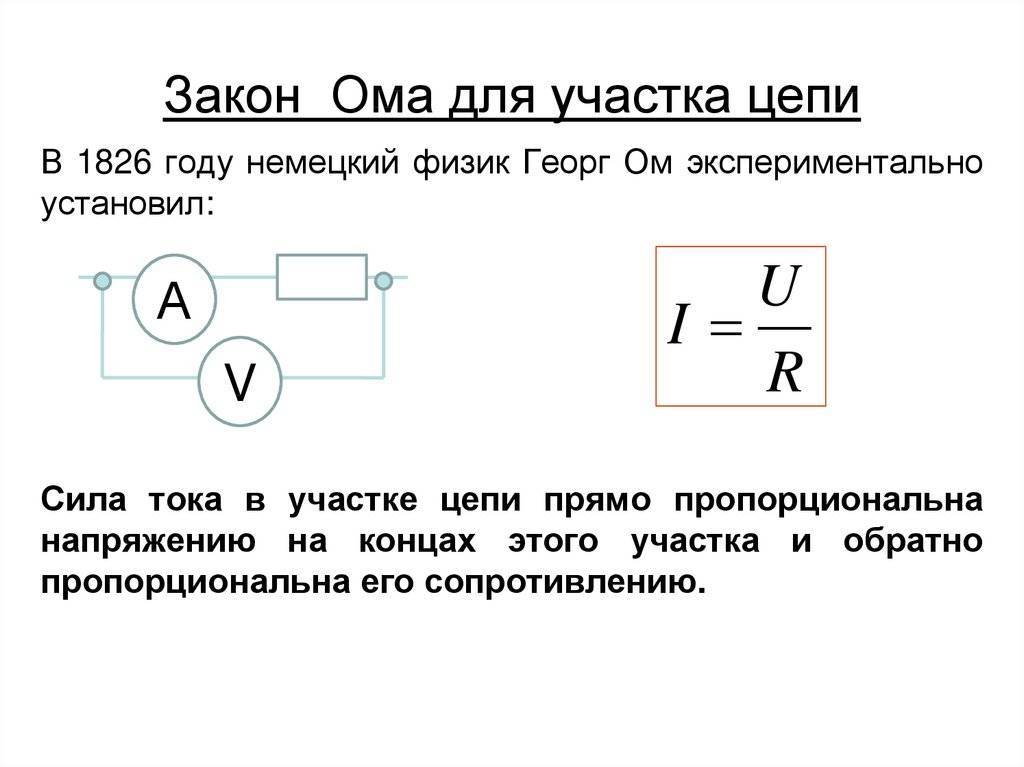
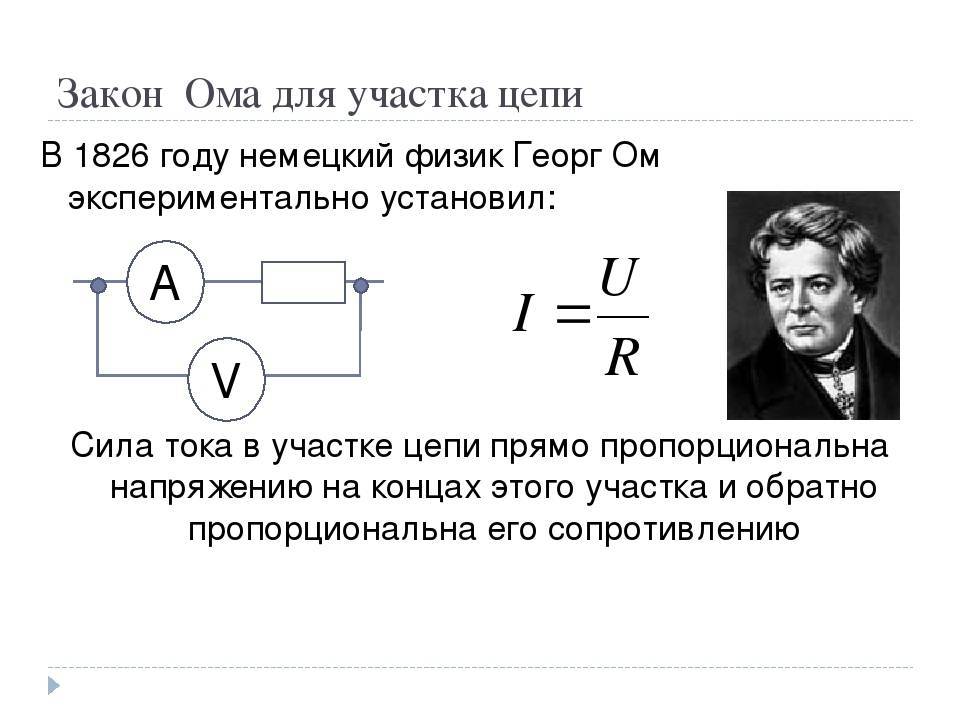
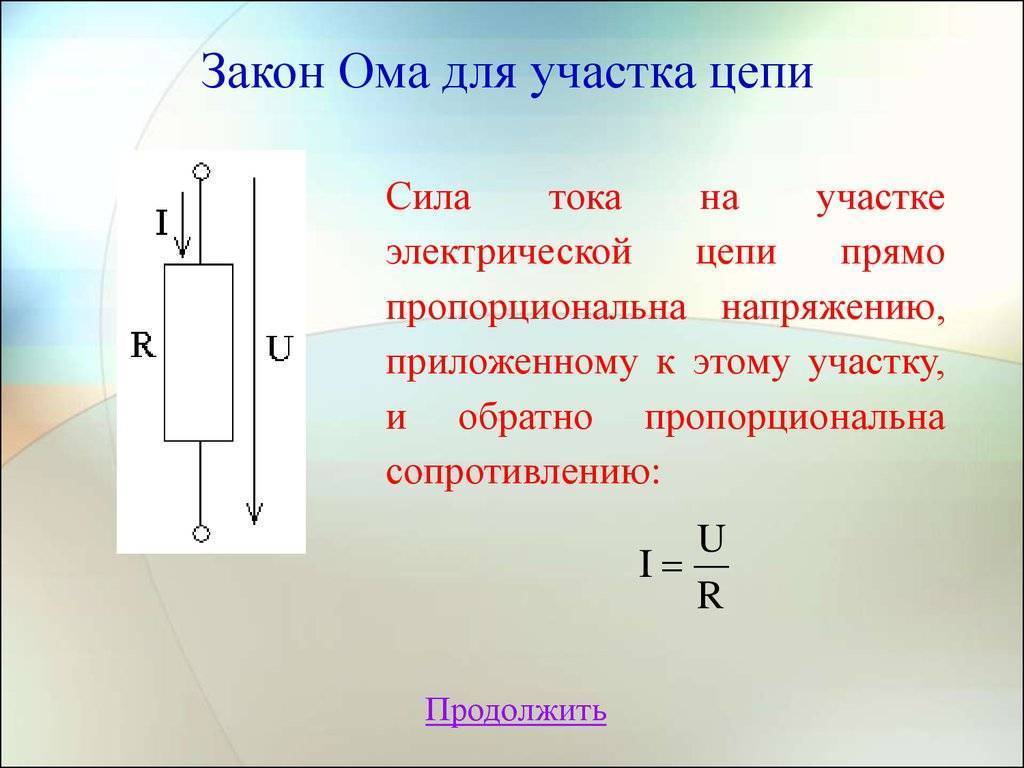
Сформулируйте закон Ома для участка цепи.
Из каких элементов состоит электрическая цепь?
Для чего служит источник тока?

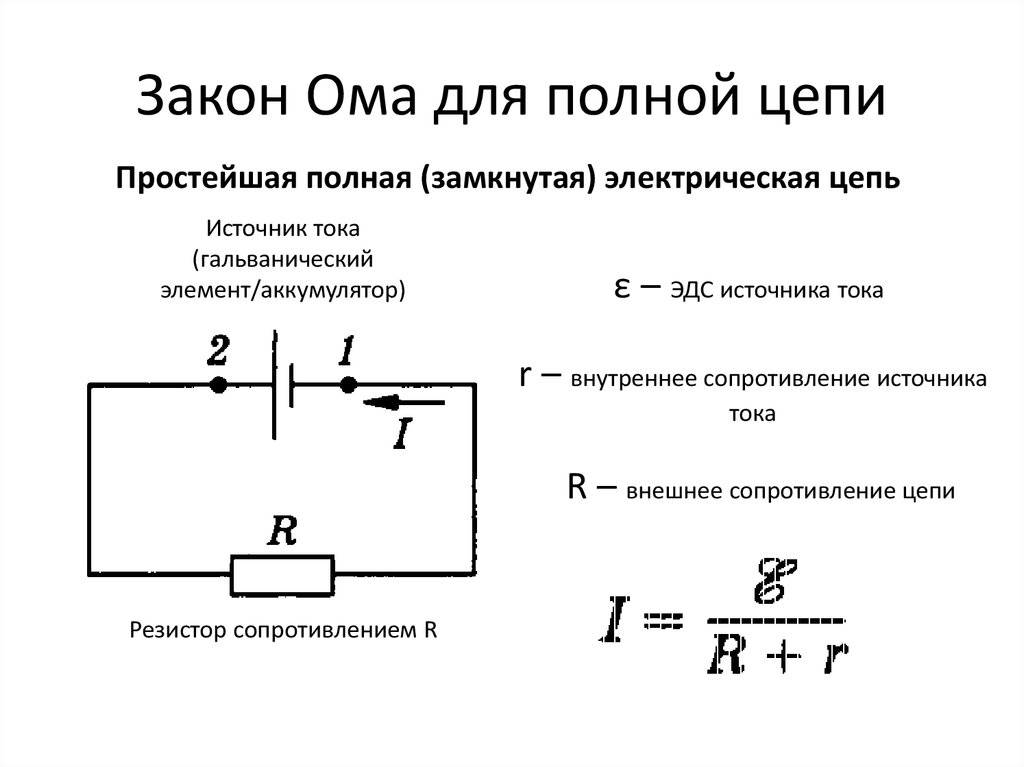
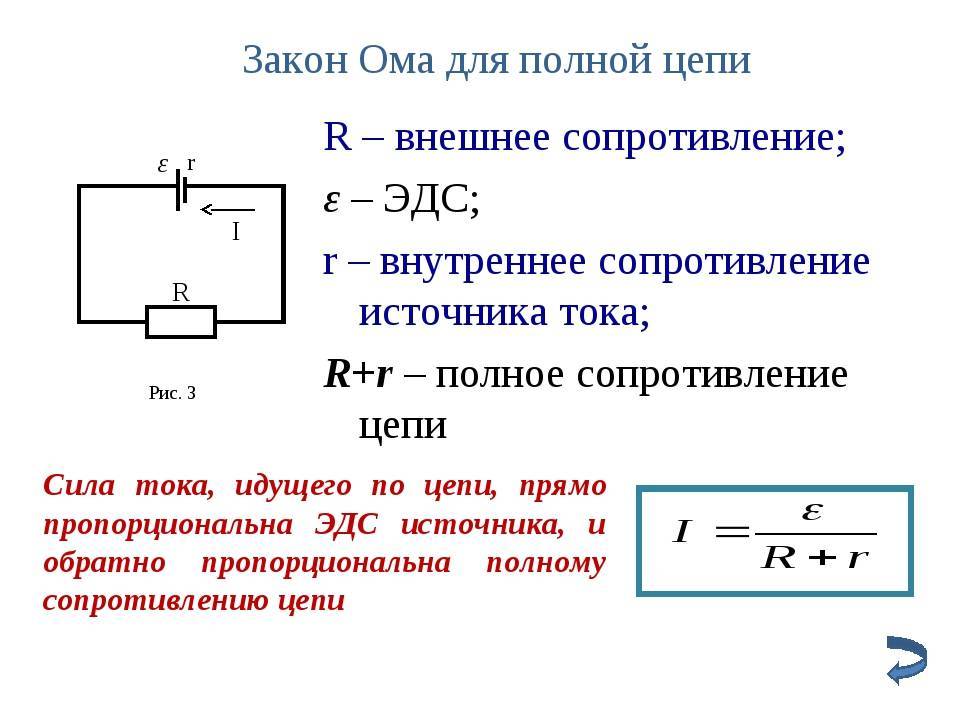
Рассмотрим простейшую полную (т. е. замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора сопротивлением R (рис. 15.10). Источник тока имеет ЭДС Ε и сопротивление r.

В генераторе r — это сопротивление обмоток, а в гальваническом элементе сопротивление раствора электролита и электродов.

Сопротивление источника называют внутренним сопротивлением в отличие от внешнего сопротивления R цепи.

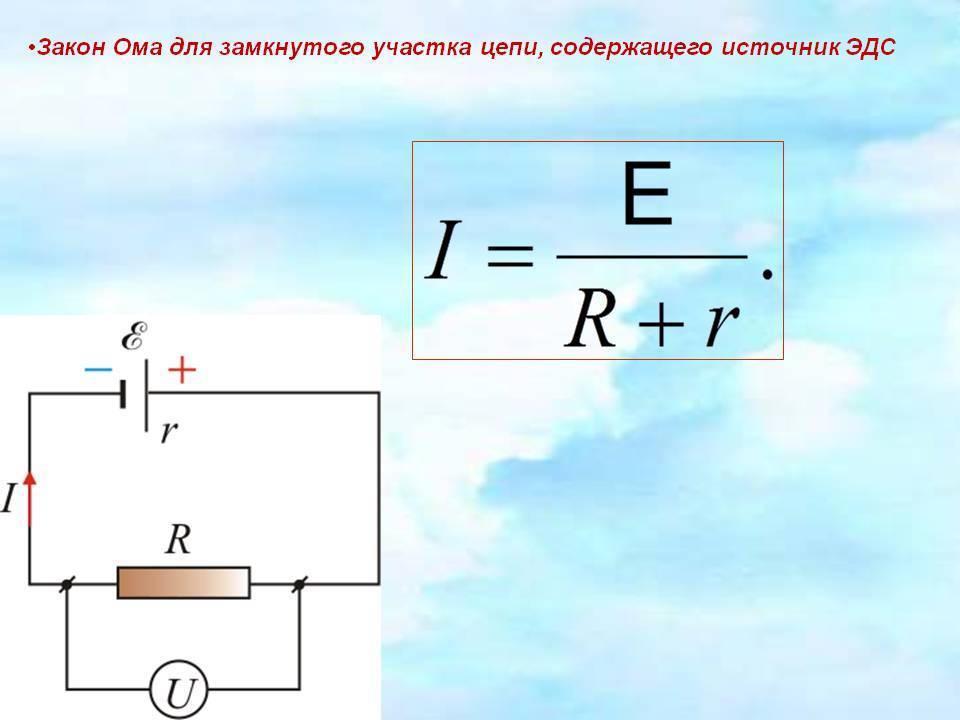
Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи R + r. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля—Ленца (15.14).

Пусть за время Δt через поперечное сечение проводника проходит электрический заряд Δq. Тогда работу сторонних сил при перемещении заряда Δq можно записать так: А_ст = ΕΔq. Согласно определению силы тока (15.1) Δq = IΔt. Поэтому

А_ст = ΕIΔt.         (15.17)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых г и Я, выделяется некоторое количество теплоты. По закону Джоуля—Ленца оно равно:

Q = I2RΔt + I2rΔt.         (15.18)

По закону сохранения энергии А_ст = Q, откуда получаем

Ε = IR + 1r.         (15.19)

Произведение силы тока и сопротивления участка цепи называют падением напряжения на этом участке.

Таким образом, ЭДС равна сумме падений напряжения на внутреннем и внешнем участках замкнутой цепи.

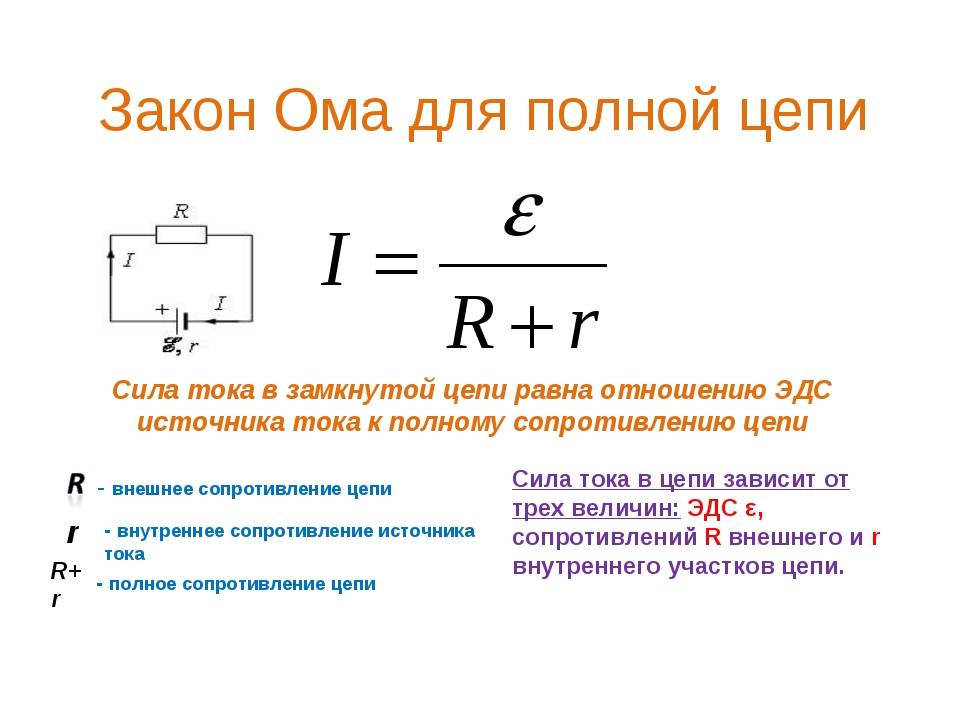
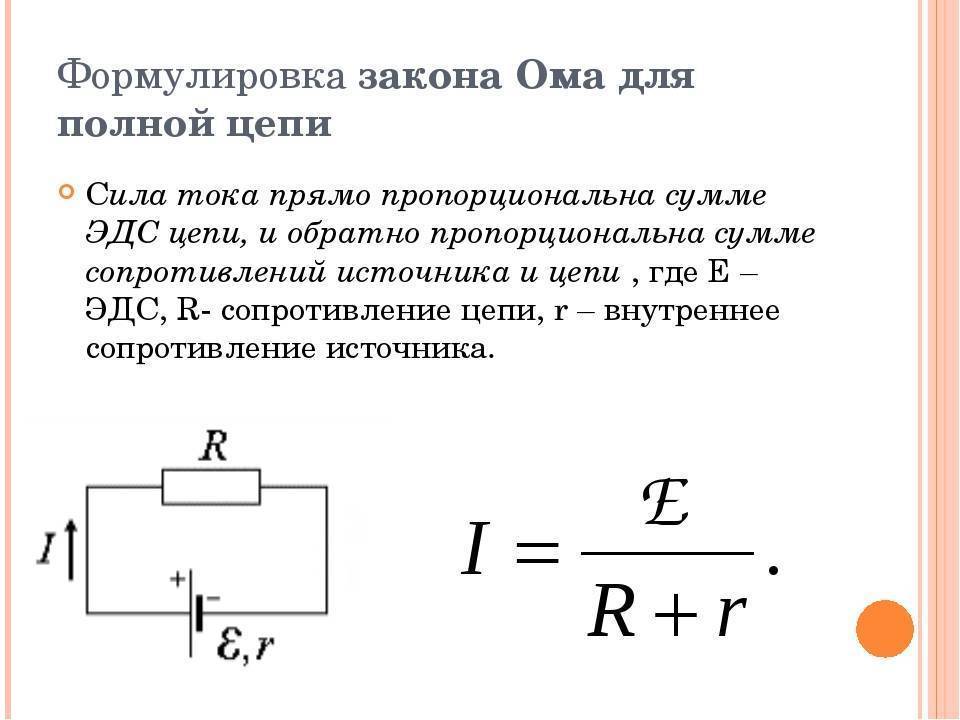
Закон Ома для замкнутой цепи:

Сила тока в замкнутой цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.

Согласно этому закону сила тока в цепи зависит от трёх величин: ЭДС Ε сопротивлений R внешнего и г внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи (R >> r). При этом напряжение на зажимах источника примерно равно ЭДС: U = IR = Ε – Ir ≈ Ε

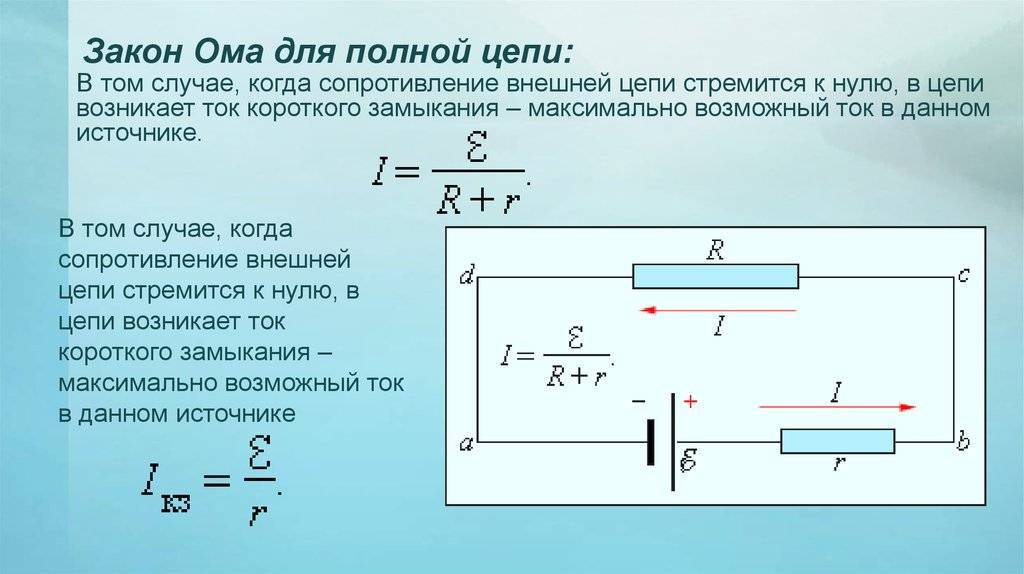
При коротком замыкании, когда R ≈ 0, сила тока в цепи и определяется именно внутренним сопротивлением источника и при электродвижущей силе в несколько вольт может оказаться очень большой, если r мало (например, у аккумулятора r ≈ 0,1 — 0,001 Ом). Провода могут расплавиться, а сам источник выйти из строя.

Если цепь содержит несколько последовательно соединённых элементов с ЭДС Ε₁, Ε₂, Ε₃ и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов.

Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура.
На рисунке (15.11) положительным (произвольно) считают направление обхода против часовой стрелки.

Если при обходе цепи данный источник стремится вызвать ток в направлении обхода, то его ЭДС считается положительной: Ε > 0. Сторонние силы внутри источника совершают при этом положительную работу.

Если же при обходе цепи данный источник вызывает ток против направления обхода цепи, то его ЭДС будет отрицательной: Ε < 0. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображённой на рисунке 15.11, при обходе контура против часовой стрелки получаем следующее уравнение:

Ε_п = Ε₁ + Ε₂ + Ε₃ = lΕ₁| – |Ε₂| + |Ε₃|

Если Ε_п > 0, то согласно формуле (15.20) сила тока I > 0, т. е. направление тока совпадает с выбранным направлением обхода контура. При Ε_п < 0, наоборот, направление тока противоположно выбранному направлению обхода контура. Полное сопротивление цепи R_п равно сумме всех сопротивлений (см. рис. 15.11):

R_п = R + r₁ + r₂ + r₃.

Для любого замкнутого участка цепи, содержащего несколько источников токов, справедливо следующее правило: алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС на этом участке (второе правило Кирхгофа):

I₁R₁+ I₂R₂ + … + I_nR_n = Ε₁ + Ε₂ + … + Ε_m

Следующая страница «Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»»

Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы постоянного тока – Физика, учебник для 10 класса – Класс!ная физика

Электрический ток. Сила тока —
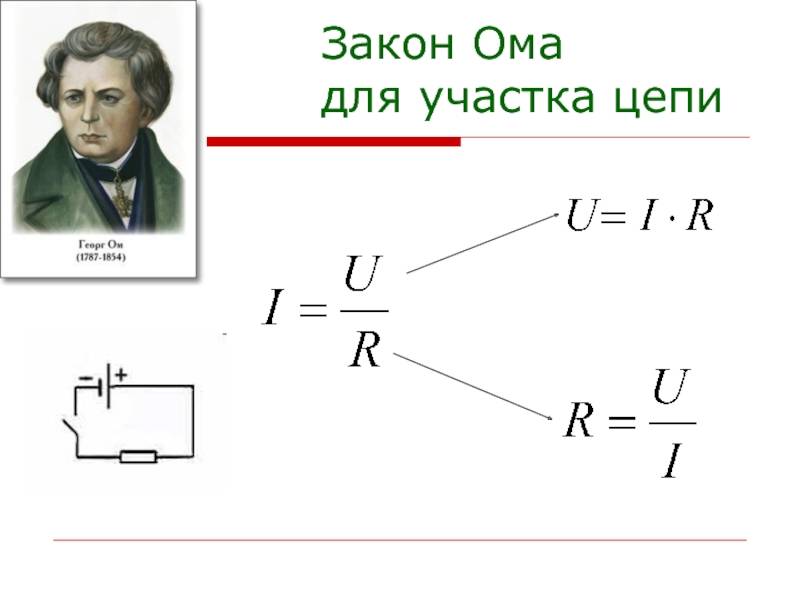
Закон Ома для участка цепи. Сопротивление —
Электрические цепи. Последовательное и параллельное соединения проводников —
Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» —
Работа и мощность постоянного тока —
Электродвижущая сила —
Закон Ома для полной цепи —
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Закон Ома для цепи постоянного тока

Классическая схема закона Ома выглядит так:

А звучит и того проще – ток, протекающей на участке цепи, будет равен отношению напряжения цепи к ее сопротивлению, что выражается формулой:

Но ведь мы знаем, что помимо активного сопротивления R, существует и реактивные сопротивления индуктивности Х_L и емкости X_C. А ведь согласитесь, что электрические схемы с чисто активным сопротивлением встречаются крайне редко. Давайте рассмотрим схему, в которой последовательно включена катушка индуктивности L, конденсатор С и резистор R:

Помимо чисто активного сопротивления R, индуктивность L и емкость С имеют и реактивные сопротивления  Х_L и X_C, которые выражены формулами:

Где ω это циклическая частота сети, равная ω = 2πf. f – частота сети в Гц.

Для постоянного тока частота равна нулю (f = 0), соответственно реактивное сопротивление индуктивности станет равным нулю (формула (1)), а емкости – бесконечности (2), что приведет к разрыву электрической цепи. Отсюда можно сделать вывод, что реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.

Сопротивление

Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.

Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.

Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.

Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.

Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.

Эту закономерность можно описать следующей формулой:

Сопротивление R = ρ · l/S R — сопротивление l — длина проводника S — площадь поперечного сечения ρ — удельное сопротивление [Ом · мм2/м]

Единица измерения сопротивления — ом. Названа в честь физика Георга Ома.

Будьте внимательны!

Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм2. При умножении мм2 сокращаются и мы получаем величину в СИ.

Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм2.

Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.

Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Получить