Классическая формулировка
Этот простой вариант трактовки, известный нам со школы.
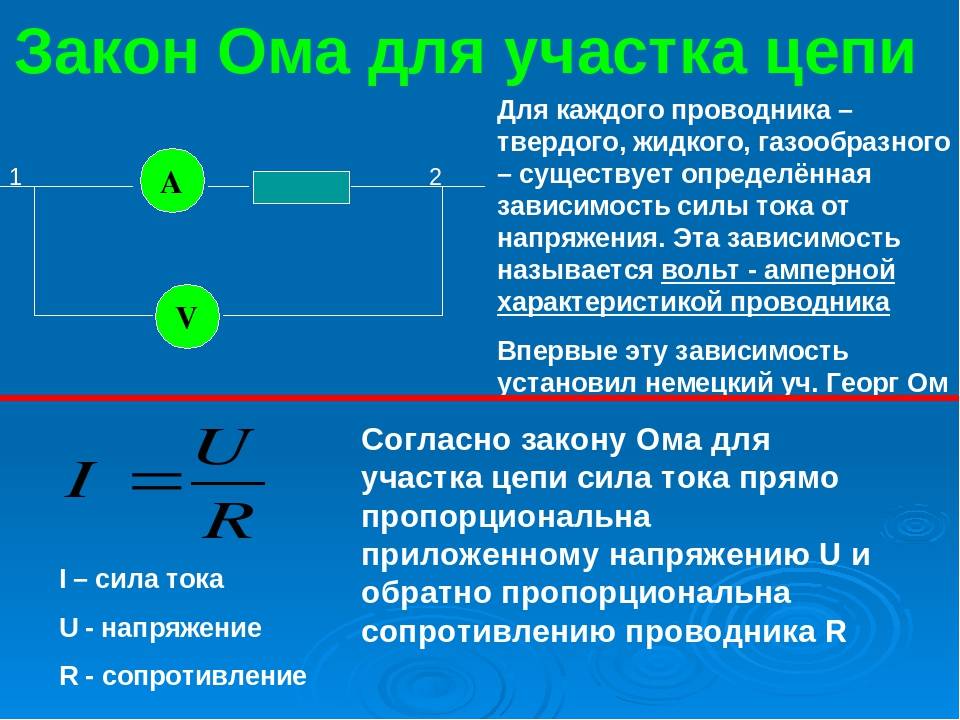
Однородный открытый участок электроцепи
Формула в интегральной форме будет иметь следующий вид:
Формула в интегральной форме
То есть, поднимая напряжение, мы тем самым увеличиваем ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I». Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.
В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.
Это интересно: Как получить 380 Вольт из 220: обзор методик
Нелинейные элементы и цепи
Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.
Физика
Пример 11. Шесть одинаковых резисторов по 20 Ом каждый и два конденсатора с электроемкостями 15 и 25 мкФ соединены в цепь так, как показано на рисунке. К концам участка подключают источник с ЭДС, равной 0,23 кВ, и внутренним сопротивлением 3,5 Ом. Найти разность потенциалов между обкладками второго конденсатора.
Решение. Между точками A и Б ток не протекает, так как между этими точками в схему включены конденсаторы. Для определения разности потенциалов между указанными точками упростим схему, исключив из рассмотрения участок АБ.
На рис. а показана схема упрощенной цепи.
Ток течет через резисторы R 1, R 2, R 3, R 4 и R 6, соединенные последовательно. Общее сопротивление такой цепи:
R общ = R 1 + R 2 + R 3 + R 4 + R 6 = 5R,
где R 1 = R 2 = R 3 = R 4 = R 6 = R.
Сила тока I определяется законом Ома для полной цепи:
I = ℰ R общ + r = ℰ 5 R + r ,
где ℰ — ЭДС источника тока, ℰ = 0,23 кВ; r — внутреннее сопротивление источника тока, r = 3,5 Ом; R общ — общее сопротивление цепи, R общ = 5R.
Рассчитаем падение напряжения между точками А и Б.
Между точками А и Б находятся резисторы сопротивлениями R 2, R 3 и R 4, соединенные между собой последовательно, как показано на рис. б.
Их общее сопротивление
R общ1 = R 2 + R 3 + R 4 = 3R.
Падение напряжения на указанных резисторах определяется формулой
U АБ = IR общ1,
или в явном виде, —
U АБ = 3 ℰ R 5 R + r .
Между точками А и Б включена батарея конденсаторов C 1 и C 2, соединенных между собой последовательно, как показано на рис. в.
Их общая электроемкость
C общ = C 1 C 2 C 1 + C 2 ,
где C 1 — электроемкость первого конденсатора, C 1 = 15 мкФ; C 2 — электроемкость второго конденсатора, C 2 = 25 мкФ.
Разность потенциалов на обкладках батареи:
U общ = q C общ ,
где q — заряд на обкладках каждого из конденсаторов (совпадает с зарядом батареи при последовательном соединении конденсаторов), q = = C 1U 1 = C 2U 2; U 1 — разность потенциалов между обкладками первого конденсатора; U 2 — разность потенциалов между обкладками второго конденсатора (искомая величина).
В явном виде разность потенциалов между обкладками конденсаторов определяется формулой
U общ = C 2 U 2 C общ = ( C 1 + C 2 ) U 2 C 1 .
Падение напряжения на резисторах между точками А и Б совпадает с разностью потенциалов на батарее конденсаторов, подключенной к указанным точкам:
U АБ = U общ.
Данное равенство, записанное в явном виде
3 ℰ R 5 R + r = ( C 1 + C 2 ) U 2 C 1 ,
позволяет получить выражение для искомой величины:
U 2 = 3 ℰ R C 1 ( 5 R + r ) ( C 1 + C 2 ) .
Произведем вычисление:
U 2 = 3 ⋅ 0,23 ⋅ 10 3 ⋅ 20 ⋅ 15 ⋅ 10 − 6 ( 5 ⋅ 20 + 3,5 ) ( 15 + 25 ) ⋅ 10 − 6 = 50 В.
Между обкладками второго конденсатора разность потенциалов составляет 50 В.
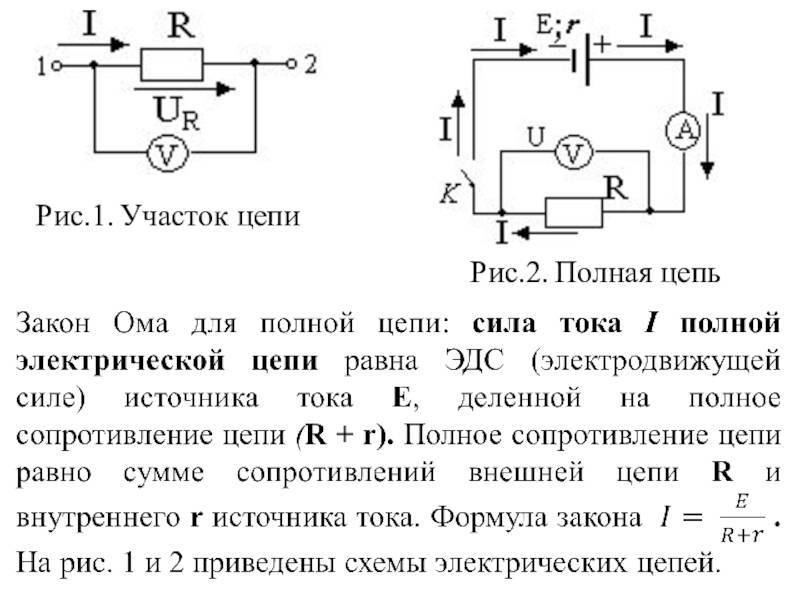
Отдельный участок и полная электрическая цепь
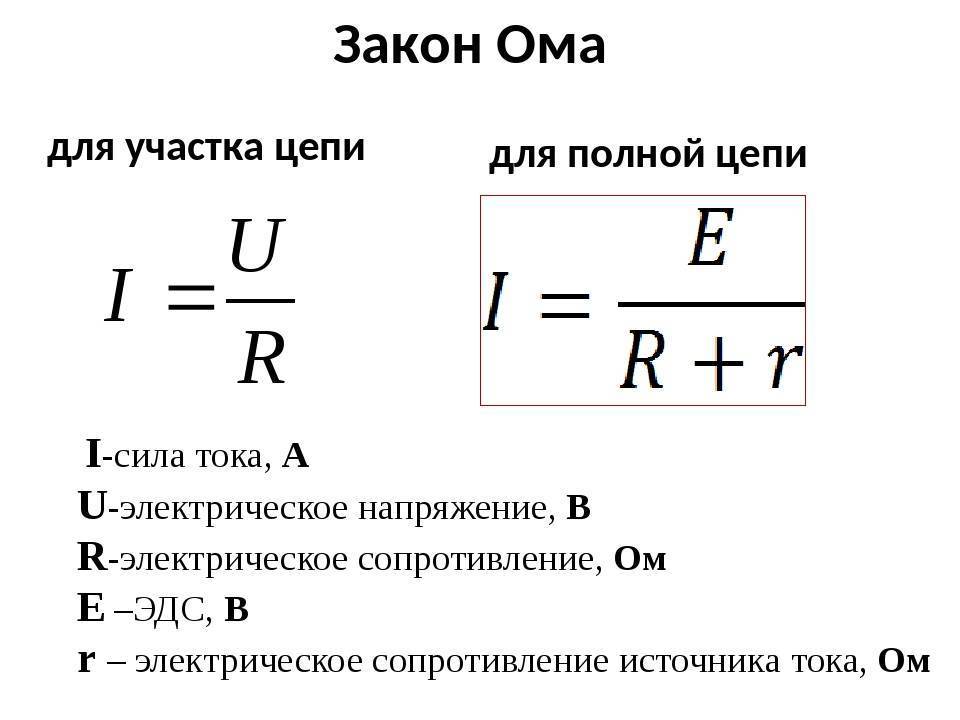
Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:
- Отдельный краткий участок. Является частью схемы без источника ЭДС.
- Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.
Расчет тока участка электрической схемы
В этом случае применяется основная формула I = U/R, в которой I является силой тока, U – напряжением, R – сопротивлением. По ней можно сформулировать общепринятую трактовку закона Ома:
Данная формулировка является основой для многих других формул, представленных на так называемой «ромашке» в графическом исполнении. В секторе Р – определяется мощность, в секторах I, U и R – проводятся действия, связанные с силой тока, напряжением и сопротивлением.
Каждое выражение – и основное и дополнительные, позволяют рассчитать точные параметры элементов, предназначенных для использования в схеме.
Специалисты, работающие с электрическими цепями, выполняют быстрое определение любого из параметров по методике треугольников, изображенных на рисунке.
В расчетах следует учитывать сопротивление проводников, соединяющих между собой элементы участка. Поскольку они изготавливаются из разных материалов, данный параметр будет отличаться в каждом случае. Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.
Вариант расчета для полной цепи
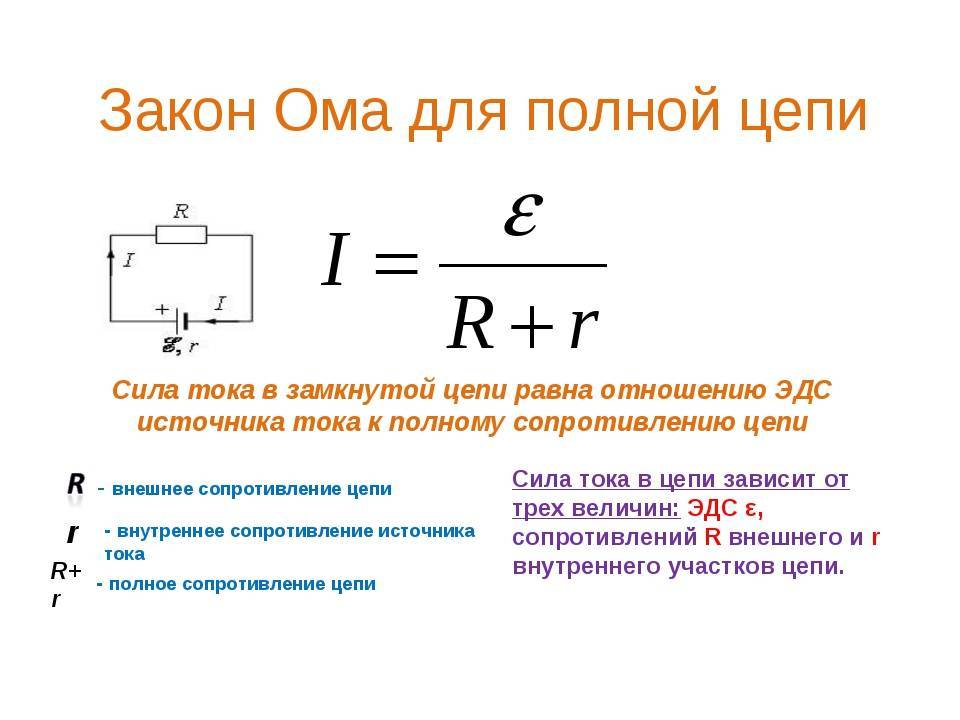
Полная цепь состоит из отдельно взятых участков, объединенных в единое целое вместе с источником напряжения (ЭДС). Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.
С точки зрения чистой физики этот показатель считается очень малой величиной. Однако, на практике, рассчитывая сложные схемы и цепи, специалисты вынуждены его учитывать, поскольку дополнительное сопротивление оказывает влияние на точность работы. Кроме того, структура каждого источника очень разнородная, в результате, сопротивление в отдельных случаях может выражаться достаточно высокими показателями.
Приведенные расчеты выполняются применительно к цепям постоянного тока. Действия и расчеты с переменным током производятся уже по другой схеме.
Действие закона к переменной величине
При переменном токе сопротивление цепи будет представлять из себя так называемый импеданс, состоящий из активного сопротивления и реактивной резистивной нагрузки. Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.
Следовательно, схема цепи переменного тока по закону Ома рассчитывается с учетом специфических эффектов: опережения или отставания величины тока от напряжения, а также наличия активной и реактивной мощности. В свою очередь, реактивное сопротивление включает в себя индуктивную или емкостную составляющие.
Все этим явлениям будет соответствовать формула Z = U / I или Z = R + J * (XL – XC), в которой Z является импедансом; R – активной нагрузкой; XL , XC – индуктивной и емкостной нагрузками; J – поправочный коэффициент.
Закон Ома для цепи переменного тока
Если рассматривать классическую электрическую цепь и на переменном токе, то она практически ничем не будет отличаться от постоянного тока, только источником напряжения (вместо постоянного — переменное):
Соответственно и формула для такого контура останется прежней:
Но если мы усложним схему и добавим к ней реактивных элементов:
Ситуация изменится кардинально. Теперь f у нас не равна нулю, что сигнализирует о том, что помимо активного, в цепь вводится и реактивное сопротивление, которое также может влиять на величину тока, протекаемого в контуре и приводить к резонансу. Теперь полное сопротивление контура (обозначается как Z) и оно не равно активному Z ≠ R. Формула примет следующий вид:
Соответственно немного изменится и формула для закона Ома:
Эмпирический характер закона Ома
При изучении природы электричества путем научных исследований происходит формулировка тех или иных законов. Они отличаются межу собой не только своим содержанием, но и тем, как были выведены. Некоторые законы представляют собой следствие из более общих утверждений, другие являются удачной попыткой объяснить многократно наблюдаемые факты.
Закон Ома для однородного участка фактически является попыткой создать правило, которое соответствует большому количеству наблюдений и экспериментов. Его формулировка на протяжении веков подтверждалась на практике, приобретая силу фундаментального закона физики. Закон Ома, представленный в интегральной форме, даёт возможность производить расчёты для различных электрических цепей.
Закон треугольника Ома
Вы можете использовать этот треугольник, чтобы запомнить закон Ома:
Треугольник закона Ома
Как использовать это:
Используйте свою руку, чтобы покрыть переменную, которое вы хотите найти. Если оставшиеся буквы расположены друг над другом, это значит, разделить верхнюю с нижней. Если они рядом друг с другом, это значит, умножить одно на другое.
Пример: нужно найти напряжение
Закрываем рукой напряжение
Закрываем V в треугольнике, затем смотрим на R и I. I и R рядом друг с другом (на одной горизонтальной линии), поэтому вам нужно их умножить. Это означает, что вы получите:
V = I * R
Все просто!
Пример: Нужно найти сопротивление
Закрываем сопротивление
Положите руку на R. Затем вы увидите, что V над I. Это означает, что вы должны разделить V на I:
R = V / I
Пример: нужно найти силу тока
Закрываем ток
Поместите руку над I. Затем вы увидите V над R, что означает деление V на R:
I = V / R
Пример 1
Лучший способ научить его использовать на своем примере.
Ниже приведена очень простая схема с аккумулятором и резистором. Аккумулятор представляет собой источник напряжения на 12 вольт, а сопротивление резистора составляет 600 Ом. Сколько тока протекает по цепи?
Пример 1
Чтобы найти величину тока, вы можете использовать треугольник выше к формуле для тока: I = V / R. Теперь вы можете рассчитать ток, используя напряжение и сопротивление:
I = 12 В / 600 Ом I = 0,02 А = 20 мА (миллиампер)
Таким образом, ток в цепи составляет 20 мА.
Пример 2
Давайте попробуем другой пример.
Ниже у нас есть схема с резистором и аккумулятором снова. Но на этот раз мы не знаем напряжение батареи. Вместо этого мы представляем, что мы измерили ток в цепи и обнаружили, что он составляет 3 мА (миллиампер).
Пример 2
Сопротивление резистора составляет 600 Ом. Какое напряжение батареи? Используя треугольник Ома (рис. 3) получаем:
V = RI V = 600 Ом * 3 мА V = 1,8 В
Поэтому напряжение аккумулятора должно быть 1,8 В.
Говорим о напряжении
Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду
Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.
На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.
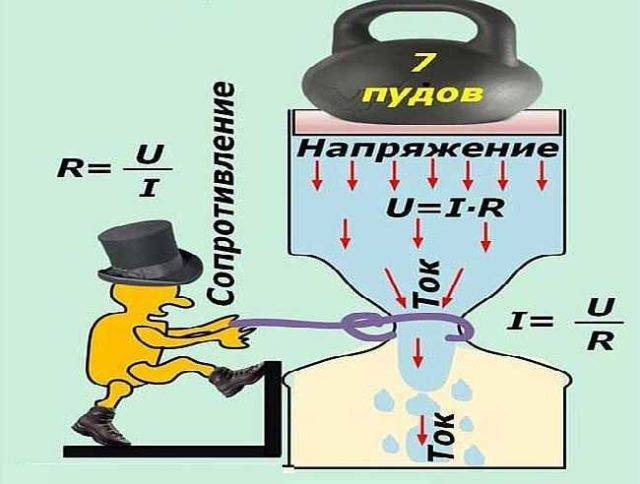
Благодаря картинке просто понять зависимость тока от напряжения и сопротивления
Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).
В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.
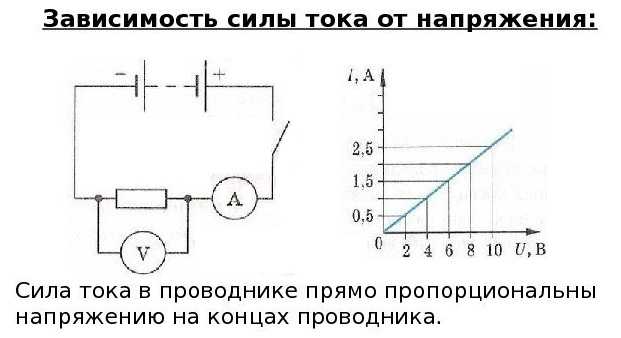
Схема для иллюстрации закона Ома
Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Формула закона Ома
Первый Закон Ома устанавливает, что разница потенциалов между двумя точками резистора пропорциональна току. Более того, согласно этому закону, соотношение между потенциалом и током всегда является постоянным для омических резисторов.
V = RI, где:
V — напряжение/электропотенциал (В);
R — электросопротивление (ом);
I — электрический ток.
Формула
В нем U является скалярной величиной и меряется в (В). Разница в электропотенциалах между двумя точками цепи, указывает на наличие электросопротивления. Когда I проходит через резистивный элемент R, происходит падение электрического потенциала. Это различие возникает из-за рассеивания энергии, называемым эффектом Джоуля. I измеряет поток зарядов через тело в (А) и прямо пропорционален сопротивлению провода.
Второй закон Ома говорит о том, что электросопротивление R представляет собой свойство из тела, которое регулирует проходимость I. Это свойство зависит от геометрических факторов тела, таких как длина или площадь сечения участка и от вызываемой величины R. Его количество зависит исключительно от материала участка.
R= ρ*L/S, где:
R — электросопротивление (Ом);
ρ — удельное электросопротивление провода (Ом.м);
L — протяженность проводника (м);
S — площадь сечения провода (м²).
Омическим резистором называется любое тело, способное представлять постоянное сопротивление для данного диапазона напряжений. График напряжения как функция тока для омических резисторов является линейным. Резистор можно считать омическим в диапазоне, в котором его потенциал линейно возрастает с ростом I.
Сопротивление можно понимать как наклон линии, заданный тангенсом угла. Как известно, тангенс определяется, как отношение между противоположным и соседним сторонами, и, в случае, когда сопротивления омические, может быть рассчитан по формуле: R = U / I.
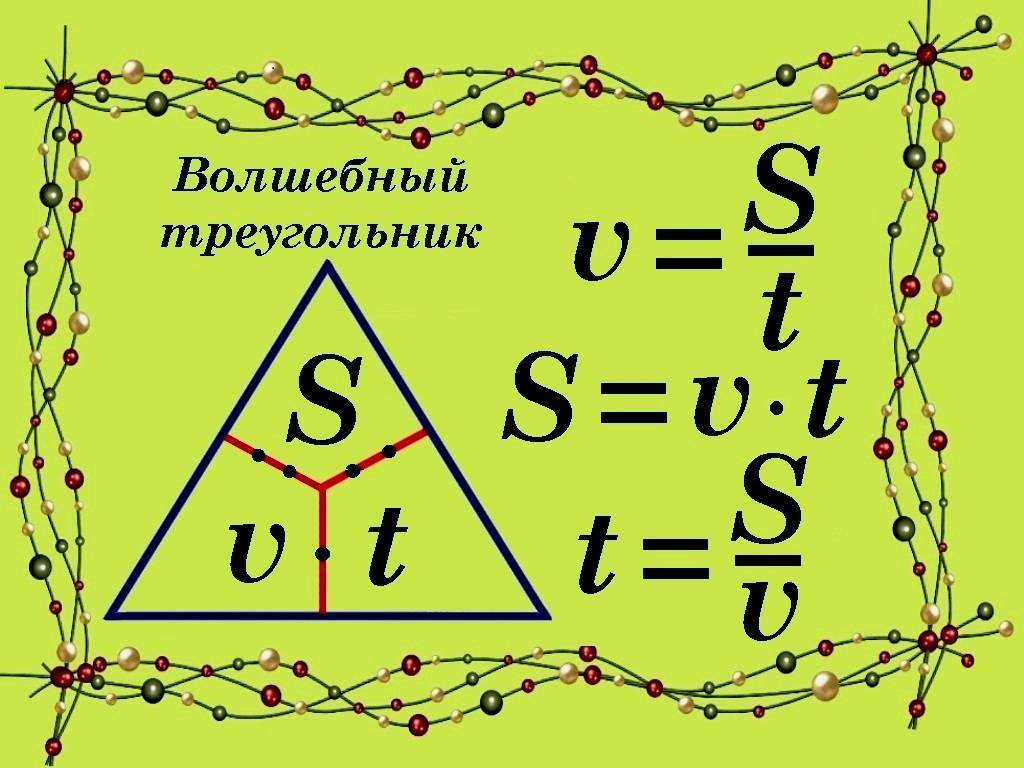Треугольник
Чтобы помочь запомнить формулу, можно использовать треугольник с одной горизонтальной стороной и вершиной вверху, как пирамиду. Это иногда называют законом треугольника Ома. В верхнем его углу находится буква V, в левом углу — буква I, а в правом нижнем углу — R.
Обратите внимание! Чтобы использовать треугольник, прикрыть неизвестный параметр, а затем, рассчитать его из двух других. Если они находятся на одной линии, они умножаются, но если одна находится над другой, их следует разделить
Другими словами, если необходимо рассчитать I, напряжение делится на сопротивление, то есть V / R.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга
Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя
Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
В общем, это наиболее распространенные варианты использования этих соединений.
Практическое использование
Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.
Применяем закон к любому участку цепи.
Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.
Находим силу тока
Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:
- Напряжение – 220 В;
- R нити накала – 500 Ом.
Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.
Рассмотрим еще одну задачу со следующими условиями:
- R=0,2 МОм;
- U=400 В.
В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА). Вычисление напряжения Для решения мы также воспользуемся законом, составленным Омом. Итак задача:
- R=20 кОм;
- I=10 мА.
Преобразуем исходные данные:
- 20 кОм = 20000 Ом;
- 10 мА=0,01 А.
Решение: 20000 Ом х 0,01 А = 200 В.
Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.
Сопротивление
Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.
Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим. Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».
Рассмотрим несколько примеров
Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.
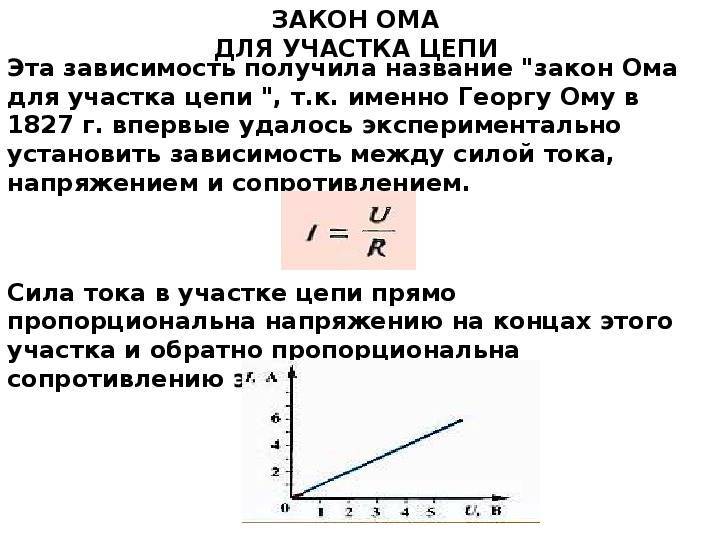
Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).
Изображение вольт-амперной характеристики, где R=1 Ом
Изображение вольт-амперной характеристики
Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).
Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении
Там где допускается обратное направление, график будет продолжен на отрицательные значения.
Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.
Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.
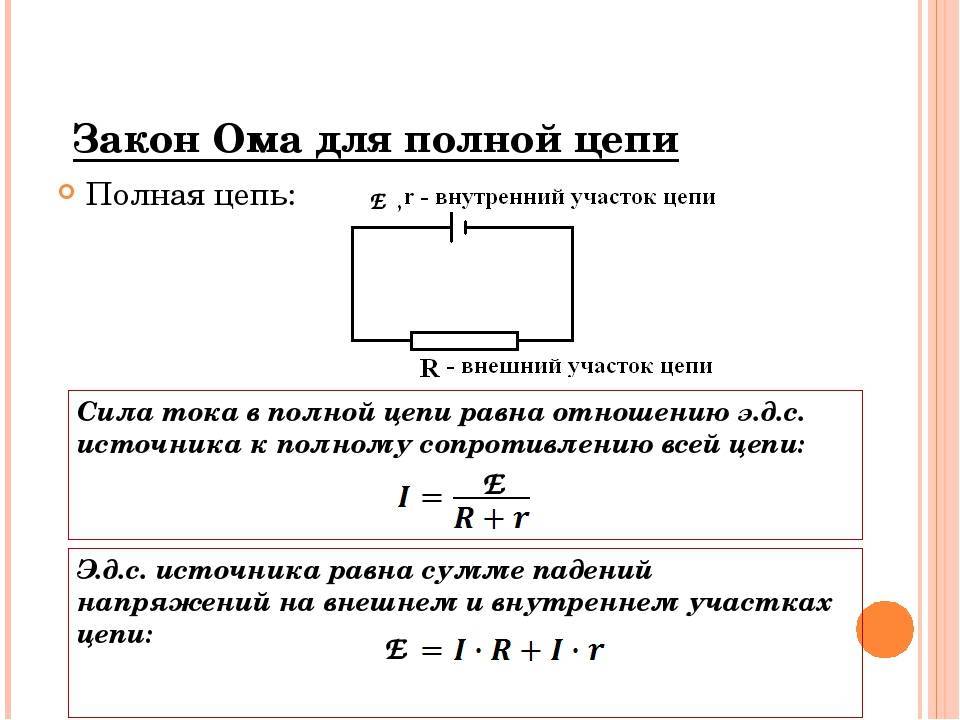
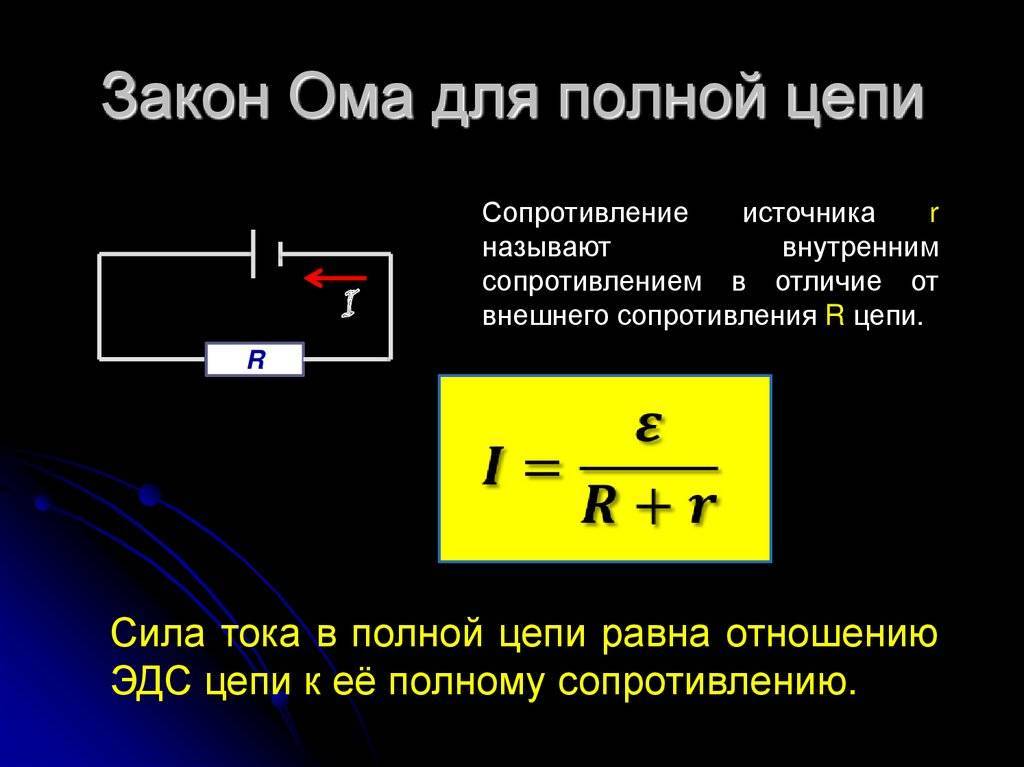
Закон ома для полной цепи
Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.
Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.
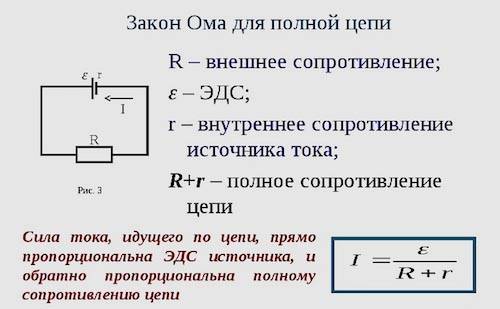
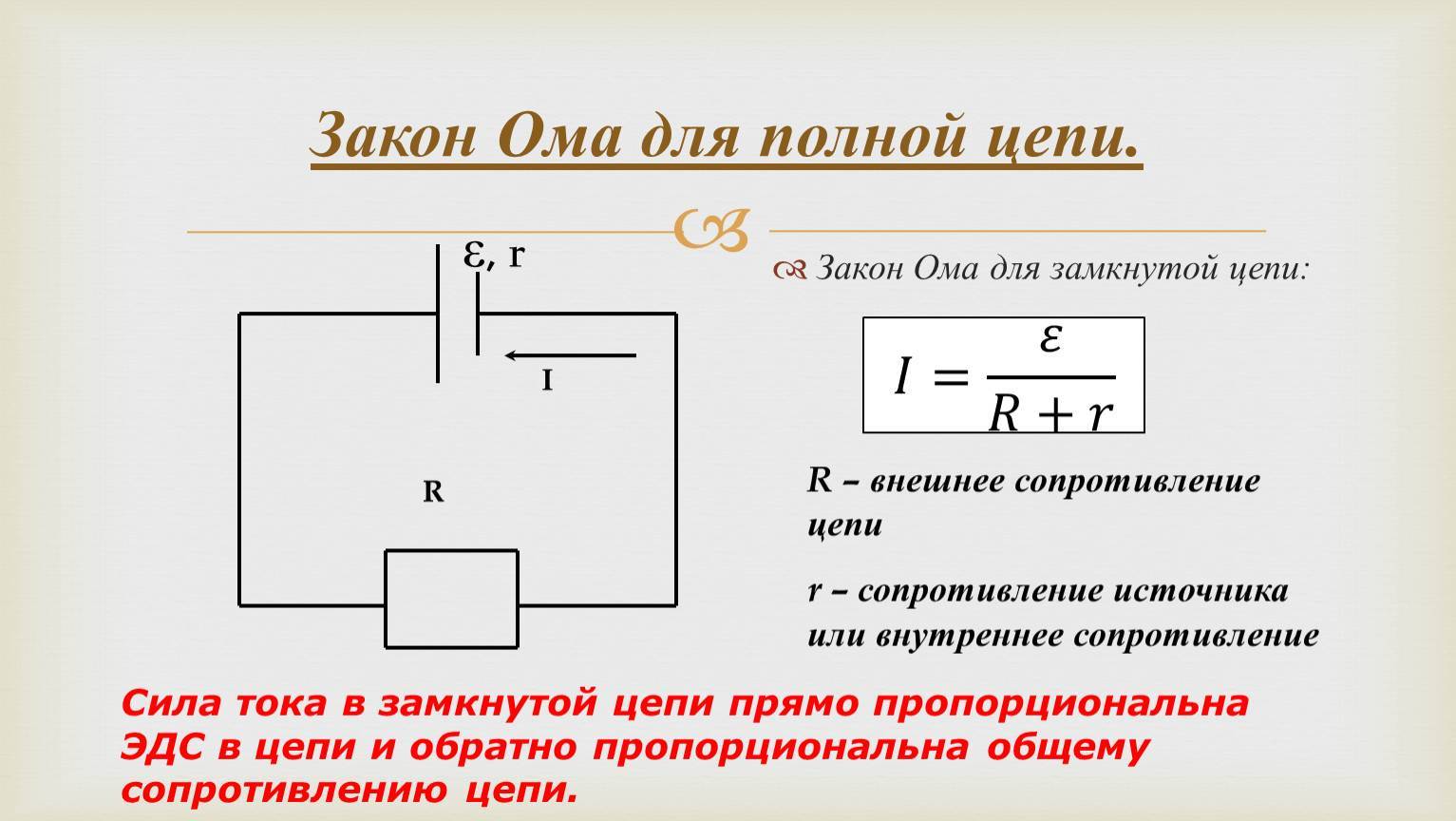
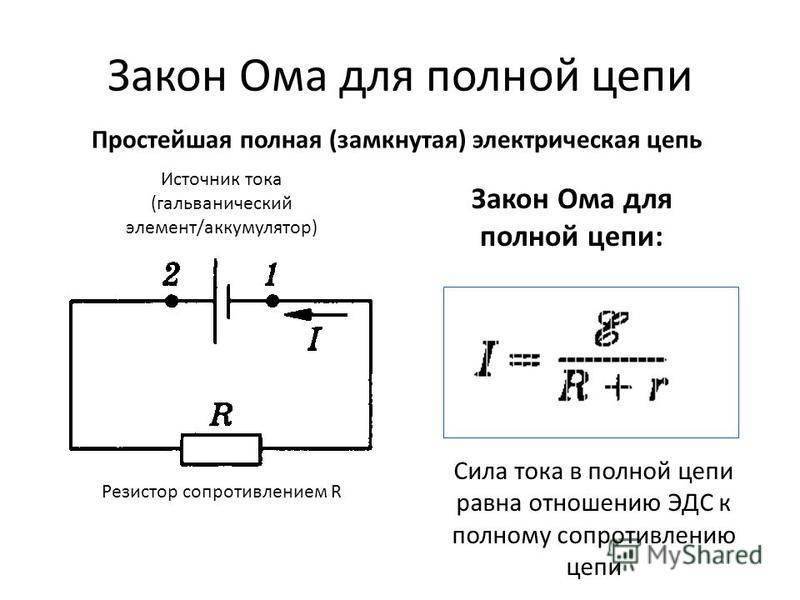
Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.
Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.
Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.
Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U < E.
ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.
Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.
Опытное определение зависимости силы тока от сопротивления при постоянном напряжении
Для того, чтобы определить зависимость силы тока от сопротивления проводника, мы проведем еще один опыт. Теперь мы будем знать электрическое сопротивление тех проводников, которые будем использовать.
Обратите внимание, что в ходе опыта напряжение на концах используемых проводников должно быть постоянным. Эта величина не должна изменяться, чтобы мы могли корректно оценить зависимость силы тока от сопротивления
Соберем электрическую цепь из источника тока, ключа, амперметра, проводника. К проводнику параллельно подсоединим вольтметр (рисунок 1).
Проводников у нас будет три разных. Они обладают разными сопротивлениями. Мы будем поочередно подключать их в цепь. Каждый раз мы будем фиксировать показания амперметра.
По показаниям вольтметра необходимо следить, чтобы напряжение на концах каждого проводника было одинаковым.
Рисунок 1. Установление зависимости силы тока от сопротивления проводника
{"questions":,"explanations":,"answer":}}}]}Закон Ома — калькулятор
Данный онлайн калькулятор закона Ома позволяет определить взаимосвязь между силой тока, электрическим напряжением, сопротивлением проводника и мощностью. Для расчета введите любые два параметра и нажмите кнопку расчет:
Для закрепления понимания работы закона Ома, приведем несколько задач для самостоятельного решения.
| Какая должна быть минимальным мощность этого резистора? Ответ:В соответствии с круговой диаграммой Р = I2*R = 0,12*50 = 0,5 Вт. Таким образом, минимальная мощность должна быть не менее 0,5 Вт, но рекомендуется взять более мощный для дополнительной надежности и долговечности. | ||
| Какой будет ток в цепи? Ответ:Это простой пример закона Ома. Напряжение и сопротивление известны, так что мы можем вычислить ток по формуле:I = V / R = 6 / 1,2 = 5 А. | ||
| Электронагреватель (резистор) мощностью 1 кВт подключен в цепь с током 10A. Какое будет падение напряжения на нагревателе? Ответ:Напряжение может быть выражено через ток и мощность по формуле: V = P / I = 1000/10 = 100 В |
